과적합 방지와 CNN
1. 과적합 방지
1. overfitting과 underfitting
과대적합 : w,b가 학습데이터에 지나치게 최적화되어 새로운 데이터에서는 다른 결과를 나타내는 현상.
학습 데이터에서는 손실이 줄어들지만 검증 데이터에서는 손실이 늘어나 예측력이 저하된다.
데이터의 특징수(독립변수 개수)가 늘어날수록, 학습 데이터 양이 줄수록 overfitting이 잘 일어나게 된다.
과소적합 : 학습데이터를 충분히 학습하지 못하여 검증 데이터만 아니라 학습 데이터에서 조차도 성능이 저하되는 현상. 학습 데이터에서는 손실이 줄어드는 과대적합과는 다르게 과소적합은 학습 데이터에서도 손실이 크다.

위 그래프는 학습이 반복되는 순서에 따라 검증 data와 학습 data의 손실 차이를 나타낸 것이다. optimum에서 가장 좋은 결과를 내고, 이 값에서 학습 반복을 멈추는 것이 가장 효과적이나 overfitting이나 underfitting이 일어나면 예측율이 저하되는 효과를 야기한다. underfitting은 최적화가 덜 되어 예측율이 저하되고, overfitting은 학습 데이터에만 너무 최적화되어 예측율이 저하된다.
2. 그래프로 보는 overfitting과 underfitting

사진 1에서 손실을 줄이기 위해 최적화한 것이 사진 2이다. 그러나 너무 학습데이터에 과도하게 최적화하여 검증 데이터를 테스트했을 때 사진 3처럼 오차가 발생하게 된다.

사진 1과 2에서는 주어진 학습 데이터가 너무 적어서 검증 데이터에서는 예측이 맞지 않는 것이다. 이렇게 주어진 학습 데이터가 너무 적을 때에는 데이터 증대의 방법을 이용하면 된다.
3. 과적합 방지
1) k-fold 교차 검증
교차 검증 : 학습용 데이터와 검증용 데이터를 분리하는데, 두 데이터를 고정하지 않고 교체하면서 검증하는 방식.
k-fold 교차 검증 : 검증 데이터를 한 세트만 만들면 이 또한 데이터세트에 과적합 될 우려가 있어 검증용 데이터도 여러 세트로 만든다.

회색 부분이 검증 데이터이며, k - 1개의 학습 데이터가 있다. 이 학습 데이터와 검증 데이터를 교체하면서 검증하여 과적합을 방지한다.
2) 가중치 정규화

가중치 정규화를 하기 앞서, 먼저 알아야 할 것이 거리함수이다. 거리 함수에는 맨해튼 노름과 유클리디안 노름이 존재하는데, 맨해튼 노름은 절댓값을 이용한 것이고, 유클리디안 노름은 제곱의 루트를 이용한다.
과적합을 방지하는 것은 가중치의 분포를 일정하게 만드는 것이다. 이를 위해 우리는 가중치 정규화, 즉 가중치 규제를 이용한다.
가중치 규제 : 가중치의 분포를 균일하게 하기 위해 가중치가 작은 값을 가지도록 패널티를 주는 것. 가중치 파라미터를 0으로 만드느냐, 0으로 만들지 않느냐에 따라 L1 정규화, L2 정규화로 나뉜다.

상단의 식과 같이 선형 함수식과 독립변수에 대한 각각의 가중치가 있으면, 위 벡터에서 가장 변화가 큰 것이 5이다. 나머지는 0 ~ 1 사이에 존재하지만 W3인 5는 이와 매우 구별된다. 따라서 이러한 값이 전체 데이터 학습을 시킬 때 복잡도에 영향을 주어 이러한 가중치를 규제한다. 우리는 L1, L2규제를 살펴볼 것이다.

좌측에 있는 게 기존 손실함수이고, 우측에 규제식을 추가하였다. 우측 식에서 람다는 hyper parameter이다. L1에서는 절댓값 이용해 가중치들의 합을 계산하며, 람다를 통해 이런 희소벡터에서의 가중치 값을 0으로 변화시킬 수 있다. L1을 W에 대해 미분하면 우측의 규제식은 x/|x|가 나오는데, 이는 w가 양수이면 양의 부호, w가 음수이면 음의 부호를 따르기 때문에 가중치 값을 0으로 변화시킬 수 있는 것이다.

여기서도 좌측이 기존 손실함수이고, 우측이 추가한 규제식이다. 람다 또한 hyper parameter이다. L2에서는 제곱을 통해 가중치의 합을 계산하며, L2 정규화와는 다르게 0이 아닌 0과 아주 가까운 값을 가중치로 둔다. L2를 W에 대해 미분하면 우측의 규제식은 람다W가 나오는데(2는 가중치에 영향을 주는 값이 아니므로 무시한다), 이를 통해 W의 값을 가중치에 적용하게 되며 가중치 갱신 식에서는 가중치를 감소시키는 방향으로 적용이 된다.
이처럼 weight decay라고 해서 가중치를 작아지는 방향으로 진행하며, 가중치의 비정상적인 성장으로 막고 올바르게 학습을 할 수 있도록 영향을 준다.
3) drop out
drop out : 과적합 방지를 위해 학습 시 지정된 비율 만큼의 임의의 입력 뉴런을 제외시킨다. 또한 드롭 아웃 정규화는 신경망 정규화의 가장 간단한 방법이다.
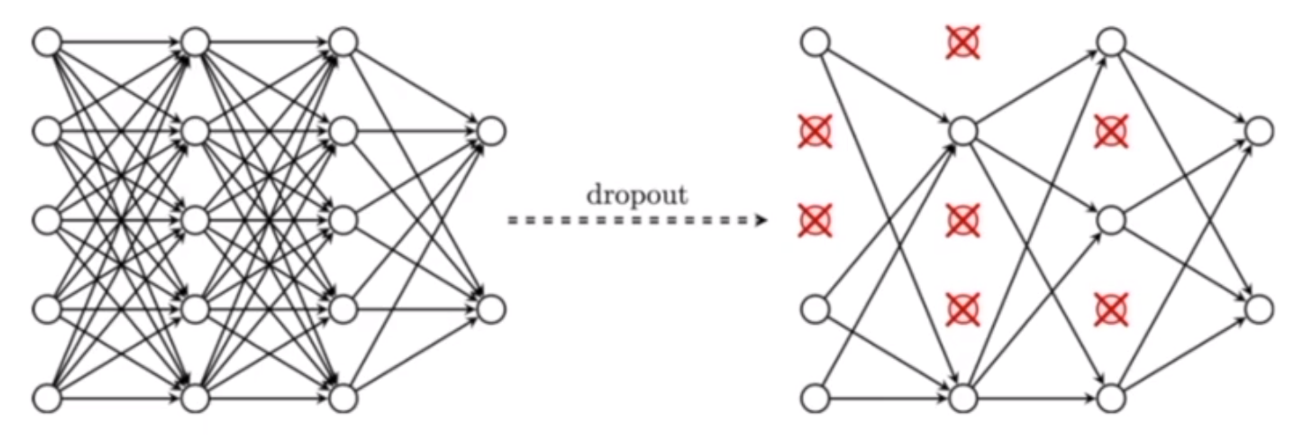
위 그림에서는 15개의 입력 뉴런 중 7개를 제외하였으니 46.6%의 입력 뉴런을 제외시켰다. 이러한 과정을 통해 과적합을 방지한다.
4) 데이터 증식
과적합의 다른 원인에는 학습 데이터의 양이 적을 경우가 있다. 일반적으로 학습 데이터셋의 샘플 개수가 충분치 않거나, 특히 모델의 파라미터 개수보다 적은 수의 데이터 샘플을 이용하는 경우 과적합이 쉽게 발생한다. 이를 방지하기 위해 데이터 증식을 이용한다.

위는 데이터 증식을 한 것의 예이다. 케라스에 있는 ImageDataGenerator를 사용해서 학습데이터의 수를 늘릴 수 있다. shift는 이동한 것, shear는 구부리는 것을 뜻한다.
5) early stopping
학습 데이터의 epochs수가 늘어나면 overfitting을 일으키며, 적은 epochs 수는 underfitting을 일으킨다. 좋은 결과가 나오면 epochs수가 남아있더라도 종료시키는 것이 early stopping이다.

이처럼 optimum에서 가장 좋은 값을 가지면 epochs수가 남아 있더라도 조기 종료시킨다. 만약 조기 종료 되지 않고 사용자가 지정해준 epochs수만큼 더 진행이 되었다면 과적화가 일어났을 것이다.
2. CNN
CNN에 대한 본격적인 설명에 앞서, CNN의 도입 배경부터 설명하려 한다. CNN의 도입 배경을 위해서는 먼저 MNIST 데이터 셋과 이 MNIST 데이터 셋을 전결합층을 통해 학습시킬 때의 단점을 알아본다.
1. CNN 도입 배경
1) MNIST 데이터 셋
MNIST는 검증 데이터 10,000개, 학습 데이터 50,000개를 가진 28*28 크기의 손으로 쓴 숫자의 SET이다. 각 출력 클래스는 0부터 9까지 10개가 존재하며, 밝기 값은 0~255 사이이다.

2) 전결합층
앞서 언급한 MNIST 데이터 셋을 전결합층을 통해 학습한다고 해보자. 알고리즘은 다음과 같다.
1) MNIST 데이터 셋을 불러온다.

2) 50,000개의 데이터를 1차원 데이터로 평면화시킨다.

3) 평면화된 각각의 데이터가 0~255사이의 값들의 SET으로 이루어져 있으므로 255로 나눠 0~1의 값으로 스케일링한다.

4) 스케일링된 데이터의 레이블 값을 to_categorical 함수를 통해 one hot encoding해준다.

이러한 과정을 통해 전결합층을 통해 mnist data set을 학습시킬 수 있다.
그러나 이 전결합층에는 치명적인 단점이 존재한다.
이미지 데이터의 경우엔 3차원 형상의 공간적 구조를 가진다. 전결합층을 이용해 MNIST 데이터 셋을 분류하는 모델을 만들 때의 문제점은 데이터의 형상이 무시된다는 것이다.
3차원의 이미지 데이터를 1차원으로 평면화시키면 공간정보가 손실되 특정 추출 및 정확도를 높일 수 없다.

위와 같은 사진이 있다고 하자.
위의 두 사진은 같은 사진이지만 평면화시키면 노란색 박스 부분인 눈부분을 확대하더라도 다르게 인식할 수 있다.
따라서 우리는 전결합층 대신 CNN을 이용한다.

2. CNN
1) CNN 구성


CNN은 위와 같이 구성된다.
convolution layer를 통해 입력 데이터의 특징을 추출해 feature map에 저장하고 pooling layer를 통해 feature map을 압축한다. CNN구성 2에서 convolution layer는 input data를 kernel을 통해 feature map을 만들고, pooling layer를 통해 feature map을 압축, 이 압축된 feature map을 flatten시킨 게 flatten layer이다. 그 뒤 만들어진 full connected layer를 softmax 함수 등을 통해 예측하거나 분류하는 기능을 한다.
뒤에서 이 과정을 자세히 설명하도록 하겠다.
2) CNN 구성 용어 - 필터, 스트라이드

필터는 위 사진에서 보듯이 가중치 행렬을 뜻한다. 만약 3차원 데이터라 채널이 존재한다면 채널에 따라 필터가 다른데, 채널이 3이면 3개의 다른 가중치 행렬, 즉 필터를 가진다. 이 필터를 통해 feature map을 작성한다. input data가 4x4이고 filter가 3x3이면 feature map은 2x2가 된다.
스트라이드는 필터를 얼만큼씩 이동시킬지를 정한다. 만약 상단 우측 사진처럼 1로 지정되었으면 필터는 1씩 이동하며, 2로 지정되면 2씩 이동하지만 위 사진에서는 입력 데이가 4x4고 필터가 3x3이니 2씩 이동할 수 없다. 만일 2씩 이동하고 싶으면 padding을 지정해 주면 된다. padding에 대해서는 뒷부분에서 설명하겠다.
3) convolution layer
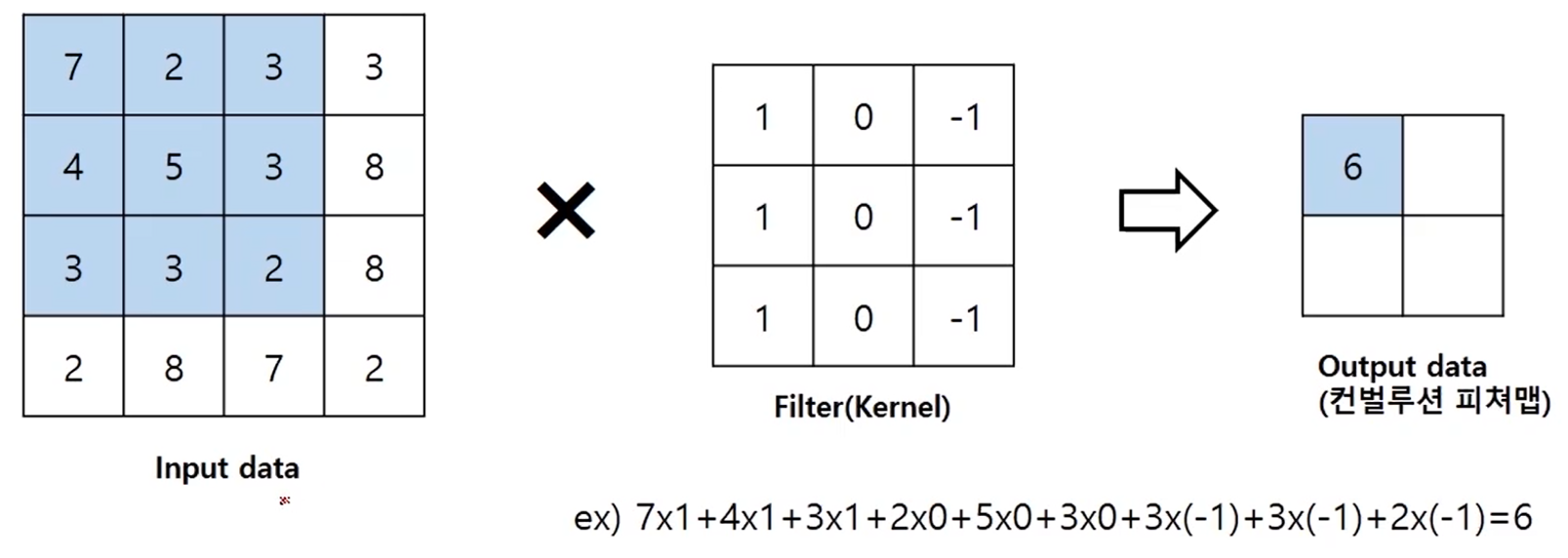
convolution은 위와 같이 계산된다. input data의 푸른색 부분(필터와 같은 3x3크기)과 필터를 위와 같은 식으로 계산하면 결과가 6이 나온다. 이 6이 feature map의 1x1자리에 자리하게 되는 것이다. 이제 스트라이드를 1로 지정해 feature map 전체를 구해 보도록 하자.
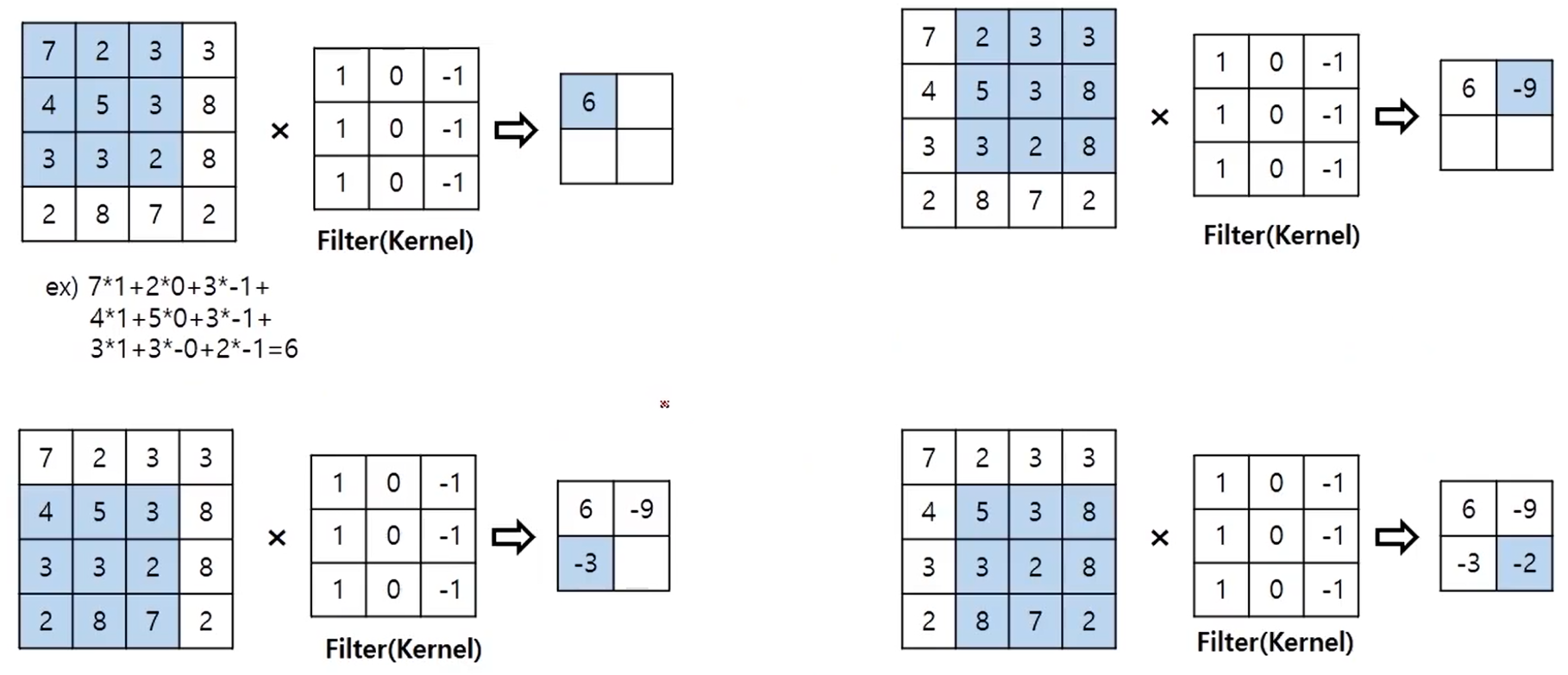
아까와 같이 모든 input data에 대해 convolution을 계산해 보면 결국 feature map은 우측 하단과 같이 구성된다.
4) Padding
padding은 convolution layer를 지날 때마다 feature map의 크기가 줄어드는 것을 막기 위해 사용된다.
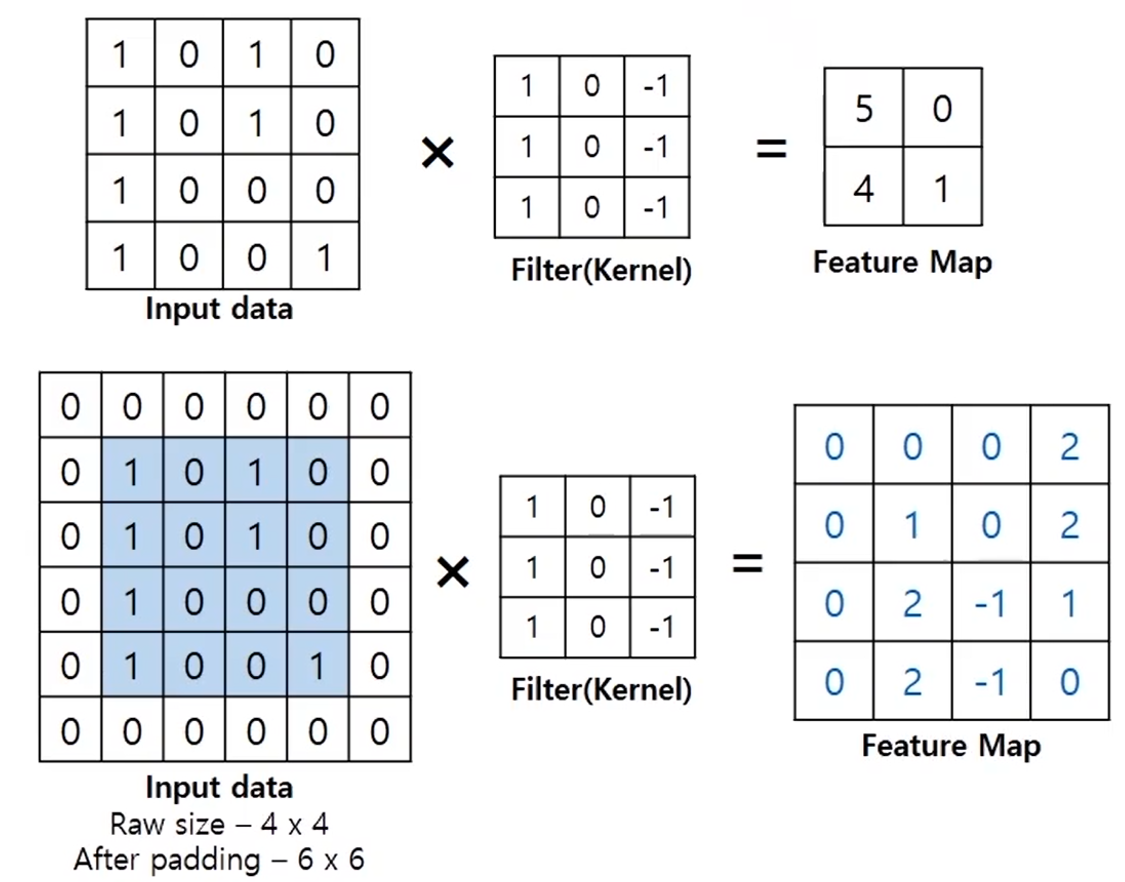
padding은 input data인 이미지의 테두리에 0또는 1을 넣어주는 것을 말한다.
상단과 같이 padding을 사용하지 않으면 feature map이 2x2의 크기가 되는 반면 padding 이용 시 연산된 feature map의 크기가 실제 input data와 같은 크기가 출력된다.
그렇다면 padding이용 시 출력 크기는 어떻게 구할까?
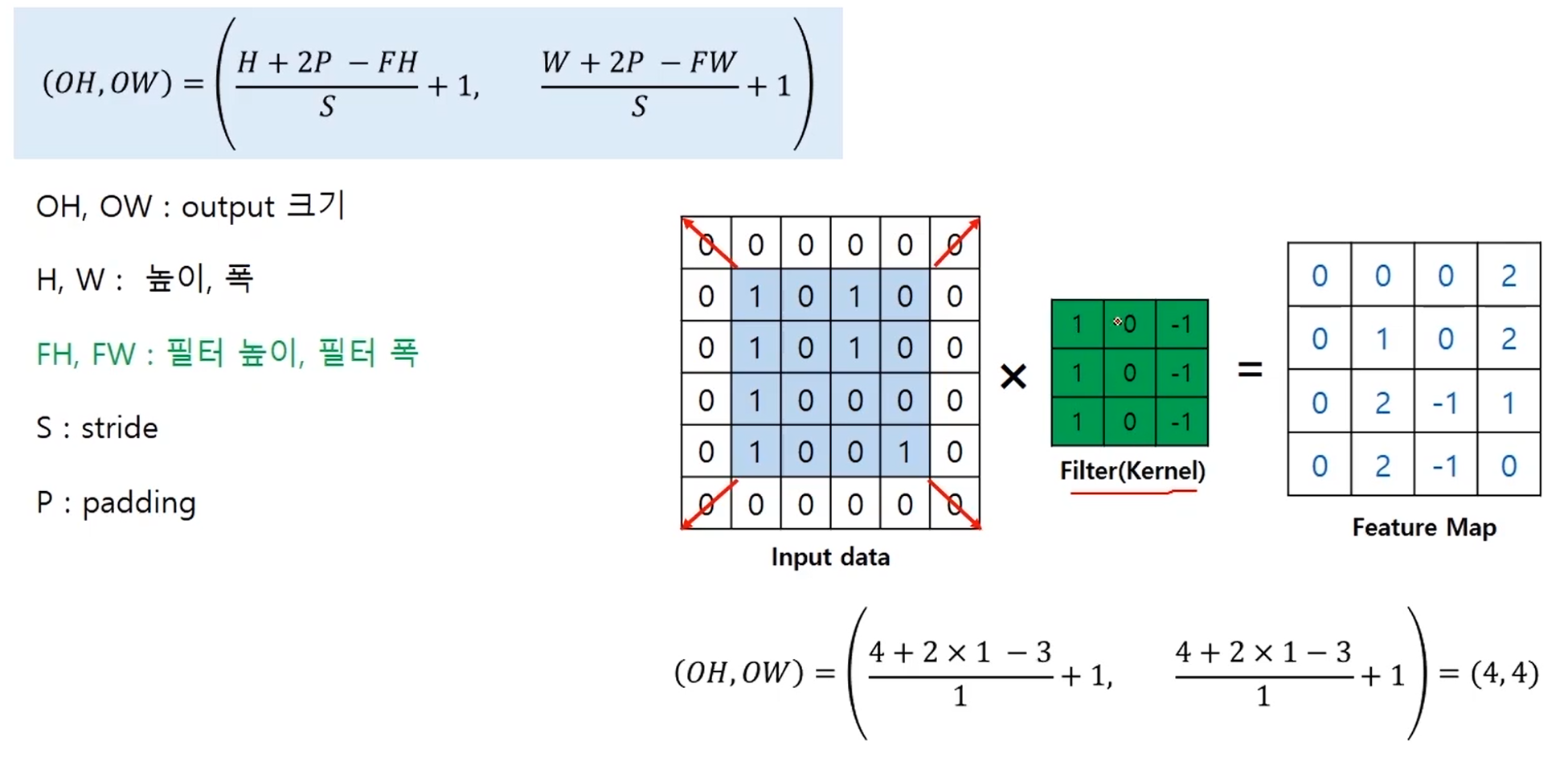
input data가 위와 같이 존재할 때, output은 위 식과 같이 표현된다. H,W는 각각 높이와 열이다. 위 식에 H,W=4, P,S=1, FH,FW=3을 대입하면 OH, OW는 4와 같은 값이 도출된다.
5) pooling layer
다음은 pooling layer이다. polling layer는 주로 convolution layer 다음에 위치해 공간을 축소시킨다. polling layer에서 convolution layer와 구분되는 점은 polling layer에서는 가중가 없고 행렬의 크기가 감소하며, 채널 수 변경이 없다는 점이다. polling에는 max pooling과 average pooling이 존재한다.

상단 좌측이 average pooling이며, 상단 우측이 max pooling이다.
average pooling은 대상 이미지 영역에서 평균값을 구하고, max pooling은 대상 이미지 영역에서 최대값을 구한다. 이들의 특징은 스트라이드 값을 2로 한다는 것이다
6) 3개의 채널에서 feature map
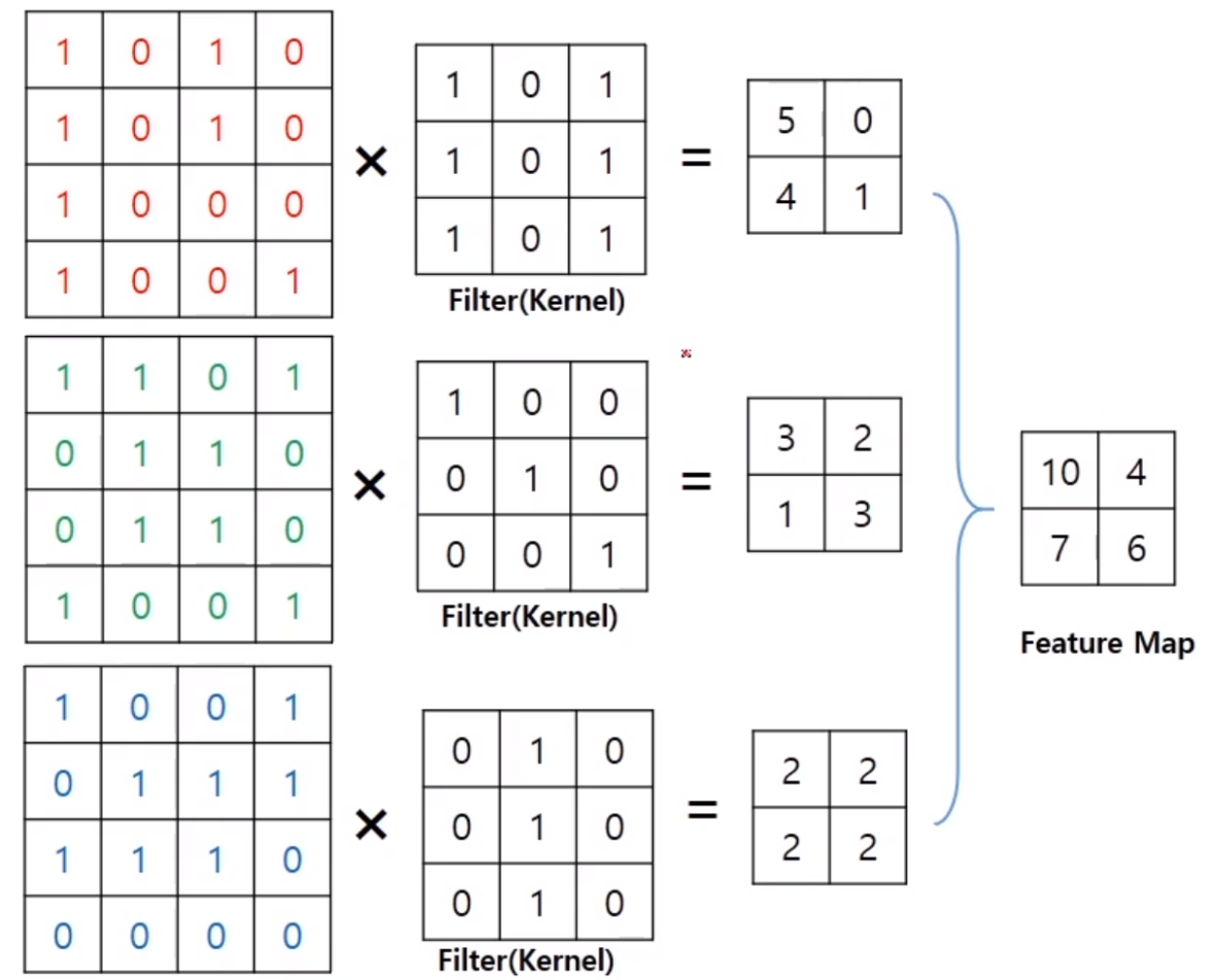
이제까지 하나의 채널에서 convolution값을 구했다면 위 사진은 RGB, 즉 3개의 채널에서의 convolution을 이용해 feature map을 구한 것이다. 각 채널마다 filter, 즉 가중치 행렬이 다른데 이는 채널마다 입력 데이터 값이 다르기 때문이다. 각 채널마다 convolution을 한 값을 더하면 feature map이 도출된다.
3. CNN, 전결합층에서의 파라미터 개수 계산

모델의 복잡도는 파라미터 개수와 직결된다. 따라서 복잡도를 계산하기 위해 파라미터의 개수를 계산한다.
먼저 전결합층에서의 파라미터 개수는 (입력 개수 + 1(bias개수))*출력 개수이다. 예를 들어 input dimension이 3이고 output이 5, bias가 1이라면 전체 파라미터 개수는 20개이다.
CNN에서 전체 파라미터 개수는 (F * F* C +1(bias 개수))+k이다. FFC는 입력인데, F는 필터 크기(정사각행렬이므로 F는 행 또는 열), C는 채널의 개수이다. 예를 들어 input shape이 32, 32, 3이고 커널 사이즈가 2,2 out filter가 10이라면 전체 파라미터 개수는 130개이다.