4기(20200711)/이론팀

벡터화, 활성화 함수 정리

KAU-Deeperent 2020. 8. 21. 23:15

[작성자 및 발표자 : 김모경]

 

1. 벡터화

일반적으로 평소에 코딩할 때 for문을 정말 자주 사용하는데, 딥러닝의 구현에 있어서는 for문의 사용은 코드 실행을 느려지게 만들 수 있습니다. numpy 내장함수를 사용하게 되면 for문을 사용할 때보다 훨씬 빨라질 수 있습니다. 그렇기 때문에 일단 for문을 쓰고 싶다면 그 공식을 쓰지 않고 numpy 내장 함수를 사용할 수 있는지 먼저 확인을 해야 합니다.

 

만약 코드를 벡터화하지 않는다면, 위와 같이 Z = wx + b를 구현하기 위하여 z = 0으로 초기화시킨 후 for문을 반복적으로 계산해야한다.  

 

반면, 코드를 벡터화했을 경우에는 파이썬의 라이브러리 함수를 통해 위와 같이 간단하게 한 줄로 표현가능하다.

 

위 코드는 로지스틱 회귀의 도함수를 구하는 코드입니다.

위 코드에서는 for문이 2번 나타납니다. (노란색 형광펜 표시한 두 부분)

 

먼저 표시된 것 중 두 번째 for문을 없애기 위해서는 dw_1, dw_2 등을 0으로 초기화하는 대신

초기화하는 부분을 지우고 dw를 벡터로 만들어야합니다. => dw를 np.zeros((n_x, 1))로 지정하여 n_x차원의 벡터로 만듭니다. 그러면 두 번째 for문인 해당 3줄을 쓰는 대신, 벡터 연산인 dw += x^(i) * dz(i) 로 바꿀 수 있다. 또한 맨 아랫줄 dw1, dw2에 대한 식을 아예 dw /= m 으로 바꿀 수 있습니다.

이렇게 두 개의 for문을 하나로 줄일 수 있게된다. 이런 식으로 벡터화는 다양한 방법으로 딥러닝에서 많은 도움이 된다.

 

 

2. 활성화 함수

활성화 함수는 인공신경망에서 입력 값에 대해서 가중치를 곱한 뒤 적용하는 함수를 의미한다.

예를 들어,

  • 계단 함수(Step Function)
  • 시그모이드(Sigmoid)
  • tanh 함수(Hyperbolic tangent function)
  • ReLU(Rectified Linear Unit)
  • Leakly ReLU
  • PReLU
  • ELU(Exponential Linear Unit)
  • Maxout 함수
  • 항등 함수(Identity Function)
  • 소프트맥스 함수(Softmax Function)

등이 있다.

 

https://bbangko.tistory.com/5

신경망은 입력층, 은닉층, 출력층으로 구성되는데, 선형함수를 사용할 경우에는 은닉층을 사용할 수 없다. 즉, 선형함수를 여러층으로 구성하더라도 결국은 선형함수를 그저 여러번 반복한 것에 지나지 않다.

위 사진을 보면 2개의 층으로 구성했지만 X에 곱해지는 항들은 W로 치환이 가능하고 입력과 무관한 상수들은 전체를 B로 치환가능하기 때문에 WX+B라는 초기와 동일한 형태를 띄게 된다. 그렇기 때문에 비선형함수를 사용해야한다.

 

위 활성화 함수의 예시들 중에서 시그모이드, Tanh, ReLU, leakyReLU 함수에 대한 그래프는 다음과 같다.

 

(1) 시그모이드(Sigmoid) 함수

시그모이드 함수는 0에 가까운 작은 값에서 일정한 유한값에 점근하는 함수로, 신경망에서 자주 이용된다. 신경망에서는 입력신호를 받아서 변환하여 전달한다.

위 그래프에서 파란색 선은 시그모이드 함수를 나타내고, 주황색 선은 미분한 시그모이드 함수의 그래프를 나타낸다.

 

시그모이드 함수 미분 과정 :

 

(2) Tanh 함수

Tanh 함수는 시그모이드 함수의 대체제로 자주 사용된다. 형태도 시그모이드와 매우 비슷하다. 시그모이드와 다른 점이 있다면 시그모이드 함수는 출력 범위가 0부터 1의 사이인 반면 Tanh 함수의 출력 범위는 –1부터 1의 사이이다. 그런데 Tanh함수는 시그모이드의 vanishing gradient 문제라는 단점을 그대로 갖고 있다.

 

 

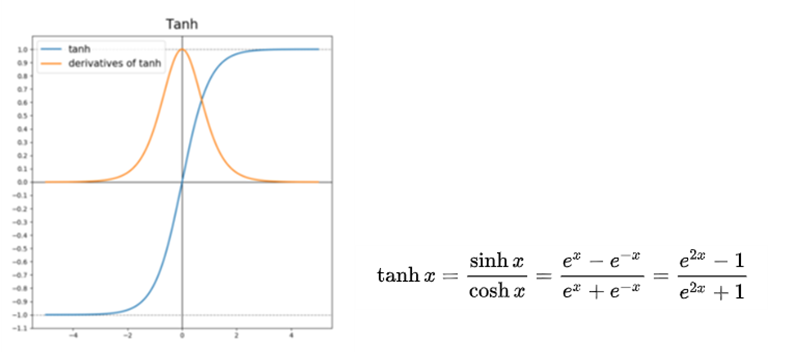
Tanh 함수 미분 과정 :

 

(3) ReLU 함수

ReLU(Rectified Linear Unit)는 입력값이 0보다 작으면 0을 출력하고, 입력값이 0보다 크면 입력값 그대로 출력하는 함수이다. ReLU는 최근 가장 많이 사용되고 있는 활성화 함수이다.

위 파란색 그래프를 보면 x > 0 일 때, 출력값은 선분의 기울기는 1인 직선의 값이다. 그리고 x < 0 일 때, 선분의 기울기가 0이고 출력값은 모두 0이다. 그렇기 때문에 ReLU 함수는 이전의 함수들에 비해 미분 값이 매우 간단하다. x > 0 일 때 ReLU 함수의 미분값은 1이고, x < 0 일 때 ReLU 함수의 미분값은 0 이다. 이렇게 ReLU 함수는 앞의 활성화 함수들에 비해서는 학습이 매우 빠르고, 연산 비용이 저렴하고, 구현이 간단하다는 장점이 있다. 하지만 입력값이 x < 0 일 때 기울기가 0이므로 뉴런이 죽을 수 있다는 단점이 있다.

 

 

(4) leakyReLU 함수

leakyReLU 함수는 입력값이 x < 0 일 때 기울기가 0이어서 뉴런이 죽을 수 있다는 ReLU 함수의 단점을 해결하기 위한 함수이다. ReLU 함수와 거의 비슷한 형태이다. 아래 식에서 0.01 대신 다른 작은 값을 사용해도 되는데 대부분 0.01로 설정한다.

 

 

 

* 활성화 함수 정리 *

 

저작자표시