모두의 딥러닝 Lec 1 ~ Lec 5 review
2021-01-08
온라인 스터디
황준성 김정민 서지민 김주안 차원범 문종연
Lab 1 review
part 1. 스칼라, 벡터, 행렬, 텐서
우리가 앞으로 다룰 가장 기본적인 스칼라, 벡터, 행렬, 텐서에 대해서 개념을 정리해 봅시다.
- 스칼라(Scalar)는 차원이 없는 숫자 하나로 이루어진 데이터입니다.(ex: x = +5)
- 벡터(Vector)의 물리적인 의미는 크기와 방향을 가지고 있으면 벡터라고 합니다. 여기서는 스칼라의 배열 이라고 생각하시면 됩니다. (ex : x = [1 , 2])
- 행렬(matrix)은 2차원의 배열입니다. 가장 대표적인 예로 가로 세로의 2차원 이미지를 생각하시면 됩니다.(ex : x = [1, 2: 3, 4])
- 텐서(Tensor)는 2차원 이상의 배열을 생각하시면 됩니다.

텐서를 제대로 표현하는 것은 매우 중요합니다. 먼저 2차원 텐서에 대해서 알아봅시다. 2차원 텐서는 [batch size, dimension]으로 표현될 수 있습니다. 아래 그림의 예시는 [64,256]이 되겠군요.

그 다음 3차원 텐서에 대해서 살펴봅시다. 가장 간단한 예로 연속된 이미지를 생각해봅시다. 2차원의 이미지가 여러 장 있다고 생각하시면 됩니다. 이 때, 표현 방법은 [batch size, width, height]로 표현할 수 있습니다.

MLP의 경우에는 [batch size, length, dimension]으로 표현합니다.

이제 기본적인 개념에 대해 이해했다면 numpy에 대해서 알아봅시다. NumPy는 행렬이나 일반적으로 대규모 다차원 배열을 쉽게 처리 할 수 있도록 지원하는 파이썬의 라이브러리입니다. 그럼 한번 예시를 들어 볼까요?

anaconda3로 pytorch와 numpy를 이용해서 위의 코드를 작성해 봅시다.
배열 t는 [0 1 2 3 4 5 6]의 1차원의 형태를 가지고 있습니다. 따라서 차원은 1이고, 총 가지고 있는 elements는 7개 임을 알 수 있습니다.
t[0]은 t 배열의 첫 번째 element를 의미합니다. 여기서 t[-1]은 마지막 배열 원소를 의미합니다.
t[a:b] 형태를 통해 배열을 잘라낼 수 있습니다. t[a:] 은 a부터 끝까지 잘라내는 것을 의미합니다.
마찬가지로 2차원 배열에 대해서도 같은 결과를 얻어낼 수 있습니다. 아래 그림은 4행 3열의 2차원 행렬을 나타낸 것입니다.

행렬의 덧셈을 해봅시다.
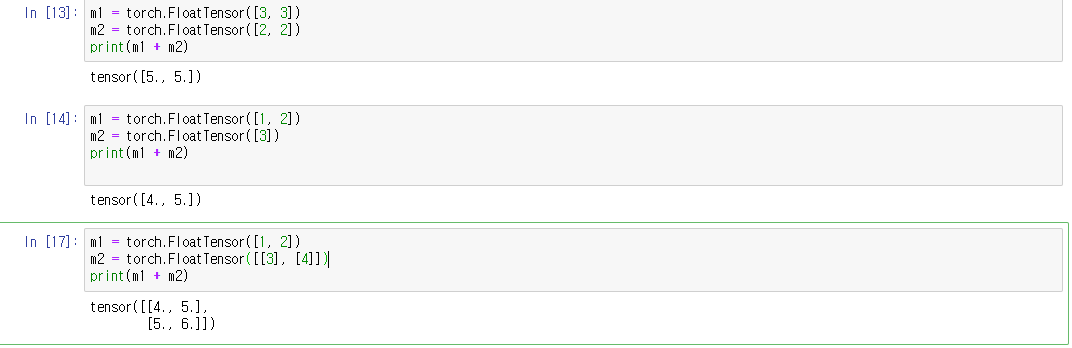
위의 코드에서 보듯이, [3, 3] + [2, 2]를 하면 [5, 5]가 됩니다. 행렬의 연산은 두 행렬의 행과 열이 같아야합니다. 하지만 만약 두 행과 열이 같지 않다면 어떻게 될까요? pytorch에서는 자연스레 행과 열을 맞춰줍니다. 예를 들어 [1,2] + [3] 이면 [1, 2] + [3, 3] =[4,5]로 맞춰주는 것과 같지요. 이를 broadcasting이라고 합니다.
이외에 여러 함수들을 알아봅시다.
먼저 평균을 구해주는 mean이 있습니다. mean을 사용해 차원의 평균을 구할 수도 있습니다.

이외에도 합을 구하는 sum 가장 큰 값을 찾는 max 등이 있습니다.

part 2
view 를 이용해 tensor의 shape를 변경할 수 있습니다. 아래는 2*2*3에서 4*3으로 변경한 화면입니다.

이외에도 squeeze, unsqeeze를 통해 차원을 짜내거나 다시 올릴 수 있습니다.

또한 tensor의 type을 바꿔줄 수도 있습니다. 1은 True, 0은 False의 2진 binary 형태로 전환할 수도 있습니다.

이외에도 concatanate를 통해 두 개의 텐서를 이어 붙이거나, ones and zeros를 통해 모든 텐서들의 원소를 1이나 0으로 만들 수 있습니다.

Lecture 2. Linear Regression
아래와 같은 data set이 있습니다.
| x | y |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
그렇다면 x = 5일 때, y의 값은 몇이 될까요? 눈치 빠르신 분들은 바로 10이라고 답하였을 겁니다. 우리는 y = 2x + 0 형태로 나타내는 그래프를 상상하고 x=5가 될 때 y는 10이 될 것이라고 예측할 수 있습니다..
기계학습에서는 모델이 학습 데이터를 받으면 임의의 선을 그어놓고 거기서부터 시작합니다. 임의의 w,b에서 부터 시작하여 H(x) = Wx + b에서 가중치 w, b를 계속해서 update하면서 실제 값과의 차이인 cost를 계산합니다. 이 때 cost function의 형태는 아래와 같습니다.

cost 가 작을수록 더 정확한 모델이 되겠군요.
즉 Linear Regression의 최종목적은 cost를 가장 작게 만들어주는 W와 b를 찾는 데에 있습니다.
b=0 이라고 하고 위의 식에서 cost와 w의 관계 그래프를 그리면 아래와 같습니다.

여기서 cost가 가장 작은 때는 w가 2일 때입니다. 그래프를 보시면 주변에서 점점 아래로 내려가는 형태를 보실 수 있습니다. 여기서 Gradient descent 방법이 제시됩니다. 임의의 지점 w에서 시작하여 미분값을 이용해서 계속해서 내려가면 됩니다.
