모두의 딥러닝2 Lec 6 ~ Lec 9 review

2021-01-16

온라인 스터디

황준성 김정민 서지민 김주안 차원범 문종연

 

Lab 4 review

part1. Multivariable Linear regression

multivariate(다변수) 선형회귀는 여러개의 입력변수로부터 결과값을 도출하는 방식입니다.
그림에 써진것과 같이 일반적인 선형회귀는 하나의 입력변수로부터 결과를 얻습니다. 반면 multivariate 선형회귀는 결과에 미치는 변수들이 여러개 존재할때 사용하게 됩니다. 
이러한 여러 변수 입력을 표현하기위해 pytorch에선 뉴럴네트워크 모듈을 사용하여 간단히 표현할수 있습니다.

 

 

 

multivariate 선형회귀의 cost function은 일반선형 회귀와 동일한 평균제곱 오차식을 사용하게됩니다.
따라서 pytorch에서 표현 할 때는 일반 선형회귀의 cost function과 같은 형태로 표현 할 수 있습니다.

 

 

앞서 설명과 같이 늘어난 변수들 갯수만큼 선언해야할 가중치의 값 역시 늘어나게 됩니다. 이를 표현하기 위해  pytorch의 뉴럴네트워크모듈을 사용할수 있습니다.
오른쪽 multivariatelinearregression 모델 클래스는 뉴럴네트워크 모듈을 상속받아 선언되었습니다. 생성자 설정영역에선 입력받는 변수의 갯수를 같이 써주는 것을 볼 수 있습니다. 
실습에선 입력의 갯수를 3과 출력 갯수 1로 두어 3과 1의 숫자로 선언하였습니다.

 

 

cost function 역시 torch.nn.functional 모듈의 mse_loss 함수를 통해 간단하게 표현 할 수 있습니다. 입력으로는
가설함수의 결과값과, 실제값을 받아 사용 할 수 있습니다.
아래는 팀스터디중 loss와 cost 함수의 정의를 이야기해 본 내용입니다.  loss함수는 데이터 하나에 대한 예측값과 
실제값의 차이를 다루는 함수라면 cost 함수는 학습중 사용된 데이터셋의 평균적인 예측과 실제값의 차이를 다룰 때 사용하는 함수라고 이해하였습니다.(쉽게 말해  loss함수들의 평균이 cost 함수라고 이해)
따라서 오차가 학습에 반영되는 형태는 cost함수꼴이며 이러한 cost함수들은 Functional 모듈을 통해 간편하게 사용가능합니다. 또한 간결한 코딩으로 오류처리에 강한 장점이 있습니다.

 

 

part2. Loading Data 

학습시 로드되는 데이터의 크기에 따라 세가지로 나눌 수 있습니다.

먼저 batch 방식은 전체 샘플 데이터 셋들의 cost 값들을 한번에 구합니다. 그 값들의 평균으로 가중치와 바이어스값을 학습하는 방식(batch gradient descent)입니다. 반면 Mini batch는 임의의 배치사이즈 만큼의 샘플 데이터 셋만 추출합니다. 그 샘플들의 cost function 값들의 평균으로 가중치와 바이어스를 학습하는 방식입니다. 마지막 stochastic은 샘플데이터 셋 하나의 cost function 값을 구합니다. 구해진 하나의 cost function 값을 통해 가중치와 바이어스 값을 업데이트 해주는 방식입니다.

 

 

 

앞선 각각의 방식들로 데이터가 추출되어 업데이트 되는 것을 스탭 또는 이터레이션이라고 합니다. 그리고 전체 샘플 데이터셋이 한번씩 학습을 마치는 것을 에폭이라고 합니다.

 

 

다음의 그래프를 통해 각각의 방식이 갖는 특징을 확인 할 수 잇습니다. 파란색의 batch방식 학습은 여러개 샘플들이 한번에 영향을 주어 학습됨으로써 부드러운 선을 띄는 반면 한 스탭을 처리하는데 많은 수의 데이터를 계산해야 하기 때문에 시간이 많이 소요된다는 단점이 있습니다. (global minimum찾지 못할 가능성)
데이터를 한 개씩 추출하는 빨간색의 스톡캐스틱 방식은 수렴의 속도는 빠른 장점이 있지만 그 수렴이 대표셩을 띠지 못해 오차율이 크다는 걸 확인 할 수 있습니다. 마지막으로 초록색 미니 배치는 batch방식보단 학습이 빠르고 스톡캐스틱보단 오차율이 높다는 특징을 가지고 있습니다.

 

 

pytorch에서는 데이터로더라는 객체를 제공하며 학습을 원하는 데이터셋을 입력해주고 배치사이즈와 셔플, 드롭 등을 설정하여 사용 할 수 있습니다.

 

 

여기나온 모델은 batch방식으로 데이터를 학습하는 방식입니다. 위의 for문은 에폭을 위한 반복이고 아래 for문은 batch size를 위한 for문으로 한번에 전체 샘플 데이터셋을 학습하기에 for문이 끝나면 전체 샘플데이터셋 모두 한번의 학습을 마치게 됩니다.

 

 

batch size를 256으로 했을 경우의 데이터 내부 구성입니다. 256개의 샘플들이 각각 28바이28의 데이터인 784개의 데이터를 가지고 있습니다.

 

 

모델의 각 영역별 기능은
view와 to함수로 데이터들의 입력형태를 맞추어 주며 선형함수를 가설함수로 두고  criterion 함수를  cost function으로 잡아 백워드와 스탭을 통해 모델을 업데이트 해줍니다.

 

Lab5 review

Logistic Regression

 

다음은 로지스틱 회귀를 설명하기 이전 선형회귀와의 비교입니다. 선형회귀는 다음과 같은 통과와 불통과 같은 이진 분류를 하기엔 한계가 있습니다. 매우 커다란 입력값을 분류하기 위해선 기울기가 수평선처럼 기울어지게 되면 다른 값들에 대한 분류 정확도가 떨어지기 때문입니다.

 

 

따라서 분류를 위해 0과 1이란 이진분류가 가능한 가설 함수가 필요합니다. 범위내에서 닫혀있으며 일정한 방향을 갖는 함수여야 합니다.

 

 

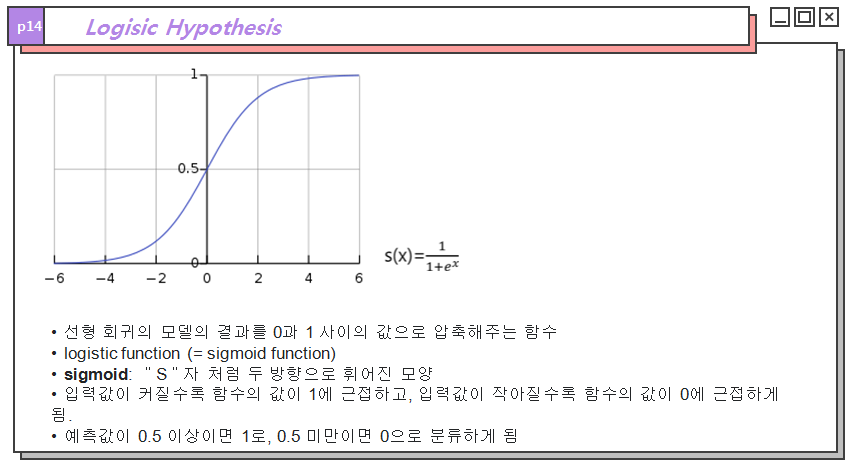
로지스틱 회귀에선 이러한 함수로 시그모이드 함수를 가설함수로 사용하게 됩니다. 시그모이드 함수는 선형함수를 통과한 결과값들이 0과 1사이의 값이 되도록 결과를 압축해줍니다. 또한 입력값이 커지면 1에 수렴하고 작아지면 0으로 수렴한다는 특징을 통해 쓰레쉬홀드를 기준으로 0과 1 2개의 값으로 이진 분류가 가능합니다.

 

 

하지만 시그모이드 함수는 그래프 특성상 울퉁불퉁한 형태를 띠며 이로인해 local minimum에 빠진다는 문제가 있습니다.

 

 

이러한 문제를 해결하기 위해 크로스 앤트로피 함수를 cost function으로 사용하게 됩니다. 예측값과 실제 정답값을 함께 사용하여 오차를 구하는 함수로 실제 값이 1이라면 왼쪽과 같은 cost function이 그려지며 실제값이 0이라면 오른쪽과 같은 cost function이 그려져 앞선 그래프보다 명확하게 오차가 최소인 점을 찾을 수 있습니다

 

 

식으로 표현한다면 마지막 식과 같이 표현 할 수 있습니다. y는 정답 값이고 H(x)는 예측값을 의미합니다.

 

 

앞선 내용을 정리하자면 로지스틱 회귀는 가설함수로 시그모이드 함수를 사용하고 cost function으로 로그손실로 크로스엔트로피를 사용하게됩니다.

 

 

로지스틱 회귀를 가지고 분류할 때는 쓰레쉬홀드를 설정할 수 있으며 값에 따라 다른 효과를 얻을 수 있습니다. 예를들어 암을 예측 할때 쓰레쉬 홀드 값에 따라 암판정 환자가 과도하게 늘어날수도 있고 조기 암판정 확률을 높일 수 도 있을 것 같습니다.

 

 

로지스틱 회귀를 pytorch에서 구현하는데는 sigmoid함수를 통해 쉽게 표현할수 있습니다. 다음 코드는 sigmoid함수를 통해 5개의 예측값을 얻어낸 코드입니다.

 

 

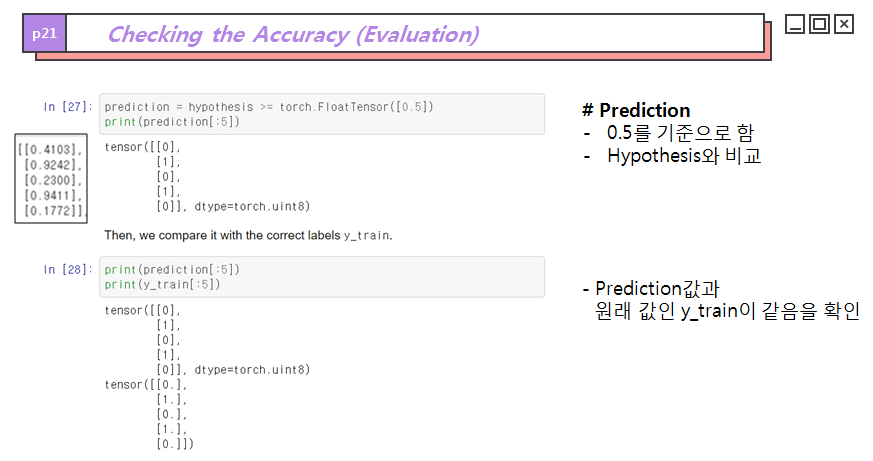
다음은 쓰레쉬홀드 0.5를 기준으로 예측값을 0과 1로 분류한 코드이며 두개는 1로 세개는 0으로 분류되었습니다.
아래쪽의 코드는 최종 예측된 분류 결과값과 실제값을 나타낸 것으로 예측과 분류과 일치하는 모습을 볼 수 있습니다.

 

 

예측의 정확도를 실습한 결과입니다.
예측 분류값과 실제값의 일치여부를 0과1로 구분하여 구분된 값을 담아주고 전체합을 갯수로 나누어 정확도를 구하였습니다.

 

 

좀더 간결한 코드작성을 위해 뉴럴네트워크 모듈을 상속받아 클래스로 만든 코드입니다.
선형함수에 입력으로 8개가 들어오면 출력으로 하나가 나가고 다시 시그모이드 함수로 들어가 값이 출력되게 선언되었습니다.

 

 

Lab 6 review

Softmax classification

다음은 softmax classification입니다. softmax classification은 오른쪽의 사진과 같이 여러 클래스들을 분류할 때 사용하는 분류방식입니다. 로지스틱 회귀의 이진분류와 달리 여러 클래스들 각각의 예측 확률을 통해 가장 높은 확률의 클래스를 최종적으로 결정하게 됩니다.

 

 

과정을 요약한다면 다음과 같습니다. 먼저 선형함수를 통해 값을 얻으며 이 값은 scores 또는 logit이라고 불리게 됩니다. scores는 소프트 맥스 함수를 통과하면서 확률로 변화게 되며 이러한 확률값중 가장 큰 확률에 해당하는 클래스가 최종 예측클래스로 선택됩니다.

여기서 다른 분류법과 비교해볼 부분은 소프트 맥스 함수입니다. 로지스틱 회귀에서 시그모이드 함수는 0과 1사이의 값으로 압축하는 것이 특징이라 한다면 소프트 맥스 함수는 선형함수의 결과값들을 비율로 분류하는 것이 특징입니다. 분류된 비율들은 총합을 1로 둔 확률로 계산되어 각 클래스별 예측될 확률로 사용됩니다.

또한 softmax함수의 형태를 살펴볼 때 지수함수와 자연상수의 특징도 확인 할 수 있습니다. 지수함수가 사용된 이유는 값에 따른 뚜렷한 구분을 위해선 지수적인 증가율이 선형적인 증가율 보다 명확하기 때문입니다. 그리고 cost함수 계산에 있어 미분 계산의 편리함을 위해 미분과 적분값이 일치한 자연상수를 사용 했다는 것을 알 수 있습니다.

 

 

 

 

다음은 softmax classification에서 cost function 계산과 학습의 과정입니다. 로지스틱 회귀와 같이 cost function 으로 크로스 엔트로피 함수가 사용되며 팀 스터디에서 조사했을 때 평균제곱오차보다 크로스 엔트로피 분류가 학습에 빠르다는 내용을 찾을 수 있었습니다. 입력되는 값은 역시 2개이며 예측확률값과 실제값이 들어가며 오차가 적을 수록 0으로 수렴하는 결과를 얻을 수 있습니다. 실제 코드 구현에선 맨 아래의 식처럼 클래스 sample 수로 나눈 평균값이 사용됩니다.

 

 

실습은 8행4열의 크기로 선언된 x값과 8개의 정답값 y를 선언하였습니다. 한번에 4개의 입력이 들어가며 최종값으로 2번3개 1번 3개 0번 2개 총 8개의 샘플 정답이 있습니다.

 

 

먼저 lowlevl의 구현에선 matmul함수, softmax함수들을 통해 가설함수 식을 직접 구현하며 zeros_like 함수와 scatter함수를 통해 직접 one-hot encoding 동작까지 표현해줍니다. cost function 역시 log함수와 sum메서드를 통해 직접 구현해주며 학습을 진행 시켜줍니다. 최종적으로 4개의 입력씩 들어가 3개의 클래스 중에서 하나를 분류하는 학습입니다. 학습이 진행 될수록 cost가 감소함을 확인 할 수 있습니다.

 

 

다음은 뉴럴네트워크 모듈을 사용하여 간결하게 작성된 코드입니다. f.cross_entropt 함수를 통해 softmax과정과 onehotencoding과정을 한번에 처리하게 되며 이는 cost function 부분에 작성되어 있습니다. 역시 에폭수가 늘어남에 따라 cost가 줄어들며 학습이 잘 진행됨을 확인 할 수 있습니다.

 

 

참고한 url

nonmeyet.tistory.com/

nonameyet

www.youtube.com/playlist?list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm

모두를 위한 딥러닝 강좌 시즌 1

www.youtube.com/playlist?list=PLQ28Nx3M4JrhkqBVIXg-i5_CVVoS1UzAv

모두를 위한 딥러닝 시즌2 - PyTorch