소프트맥스 회귀와 군집분석
발표자 : 김연주
소프트맥스 회귀
소프트맥스 회귀에 대해 알아보기 전에 로지스틱 함수에 대해 명확히 아는 것이 도움이 되기 때문에 먼저 로지스틱 회귀에 대해 간단히 알아보겠다.
1. 로지스틱 회귀
로지스틱 회귀에서는 Z의 값을 WX + B로 둔 뒤 이 Z를 sigmoid함수에 대입힌다. sigmoid함수는 예측값을 0에서 1사이의 값으로 만들어 주기 때문에 만약 이 예측값이 0.5보다 크면 class 1으로, 작으면 class 2로 분류된다. 아래의 그림에선 예측값이 0.75로, 0.5보다 크기 때문에 class 1으로 분류되었다.

그렇다면 3개 이상의 클래스로 분류하는 소프트맥스 회귀에서는 어떤 과정을 거쳐 분류하게 되는지 알아보자.
2. 소프트맥스 회귀
소프트맥스 회귀는 이진 분류가 아닌 여러 개의 클래스로 분류하는 다중 클래스 분류 문제에 사용되는 기법이다. 분류해야 하는 k개의 클래스가 있을 때, k 차원의 벡터를 입력 받아 각 벡터의 클래스에 대한 확률을 추정한다.
로지스틱 회귀는 2개의 선택지 중 하나의 선택지를 고르는 모델이었다면, 소프트맥스 회귀는 세 개 이상의 선택지 중 하나를 고르는 모델이다.
<예시>
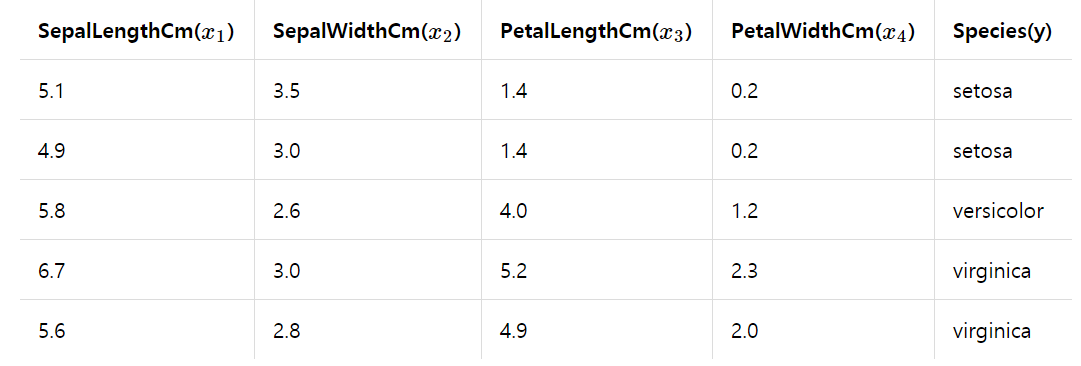
위는 꽃받침의 길이, 넓이, 꽃잎의 길이, 넓이를 이용해 분꽃의 종이 setosa, versicolor, virginica 중 무엇인지를 분류하는 예시이다. 꽃받침의 길이, 넓이, 꽃잎의 길이, 넓이를 특징(feature), 즉 독립변수 X1 ~ X4라 하고, 종을 종속변수 y로 두었다.

소프트맥스 회귀는 위와 같이 표현된다. 소프트맥스 회귀의 특징은 각 class가 될 확률을 할당하고 그 확률의 합이 1이 된다는 것이다. 위 그림에서는 class 1이 될 확률이 0.15, class 2는 0.75, class3가 0.25로 class2에 분류될 확률이 가장 높다.
또 여기서 WX+B인 Z가 특정 함수를 통해 원소의 합이 1이 되도록 만들어지는데, 이 특정 함수를 소프트맥스 함수라고 한다.
3. 소프트맥스 함수(softmax function)
k차원의 벡터에서 i번째 원소를 zi, i번째 클래스가 정답일 확률을 pi로 나타낸다고 했을 때, 소프트맥스 함수를 이용한 pi의 정의는 아래와 같다.

예시로 든 분꽃 분류 문제에서 k의 값은 3이므로 (분류해야 할 종의 종류의 개수)3차원 벡터 z = [z1, z2, z3]의 입력을 받으면 소프트맥스 함수는 아래와 같은 확률 pi를 반환한다.

여기서 p1, p2, p3는 각각의 클래스로 분류될 확률이다. P1은 virginica로 분류될 확률, p2는 setosa로 분류될 확률, p3는 versicolor로 분류될 확률을 의미하며, 소프트맥스 함수에 의해 각각의 확률의 총합은 1이 된다. 이 내용을 다시 수식으로 정리해보면 아래와 같이 나타낼 수 있다.

4. 분꽃 분류에 소프트맥스 함수 적용

이 그림에서는 batch size를 1로 두고 sample data를 하나씩 입력받았다.
여기에서 따져야 할 점은 두가지다. 첫번째는 가중치 연산방법을 통한 차원 변환이며, 두번째는 오차 계산 방법 – one hot encoding이다. 먼저 차원 변환부터 알아보자.
1) 차원 변환
아까 앞에서 언급했듯이 소프트맥스 회귀는 분류해야 하는 k개의 클래스가 있을 때, k 차원의 벡터를 입력 받아 각 벡터의 클래스에 대한 확률을 추정한다고 했다. 그러나 이 분꽃 분류 문제에서는 꽃받침의 길이부터 꽃잎의 넓이까지 총 4개의 차원(x1~x4까지)을 입력받는다. 하지만 우리는 분류해야 하는 종류의 개수가 3개이므로 3차원의 벡터를 입력받아야 한다. 그렇기에 우리는 특정 가중치 연산방법을 통해 입력 벡터의 차원을 k차원으로 변환한다. 이 때 변환한 3차원의 벡터를 z라고 표현한다면 아래와 같이 표현된다.

샘플 데이터 벡터를 소프트맥스 함수의 입력 벡터로 차원을 바꿀 때(4차원->3차원), 우리는 가중치 곱을 이용한다. 그림에서 보듯이 필요한 w의 개수(화살표 개수)는 4*3인 12개이며, cost function을 이용해 cost를 줄여나갈 때 이 w의 값이 변화하게 된다.
분꽃 분류 문제를 벡터의 곱들을 이용해 증명해 보자.
사용자가 입력한 data set을 X라고 두었는데, 변수의 형식으로 계산하는 게 편리해 오른쪽 형식으로 바꾸었다.

입력 데이터가 5개이고, 차원은 4차원인 것을 확인할 수 있다. 3종류로 분류하기 위해 가중치를 3*4인 12개로 하고, z를 x,w,b에 대한 식으로 나타내 보면

위의 식이 된다. 위의 식은 하나의 batch에만 따른 것이고 문제에서는 5개의 set을 받기 때문에 실제로는 3 x 1 행렬이 아닌 3 x 5행렬이 나온다. 밑의 식은 z를 5개의 batch 모두에 적용한 것이다.

이 식이 되며, 소프트맥스 함수에 이 z를 대입한 예측값 ^y의 값은 아래와 같다.

2) One hot encoding
소프트맥스 회귀는 각 class에 대한 확률을 나타내는데 0과 1사이의 값을 가진다고 명시했다. 학습을 통해 예측값을 실제값에 가깝게 변화시킬 수 있는데, 그럼 이 실제값을 표현할 수 있는 방법이 있어야 한다. 이 실제값을 나타내는 방법을 one hot encoding이라고 한다.
분꽃 분류 문제에서 우리는 class가 virginica, setosa, versicolor가 있다는 것을 알 수 있다. 아래의 그림은 각 class에 대한 one hot encoding이다.

이 실제값의 one hot vector와 예측값을 비교해 소프트맥스 회귀의 cost function인 categorical cross entropy를 수행해 cost를 줄여 나간다.

이 오차로부터 w와 b를 update해 오차를 줄여 나가는 학습을 하게 된다.

5. Categorical cross entropy
앞서, 이진 분류에서는 binary cross entropy라는 cost function을 통해 오차를 줄이는 학습을 하였다. 이 소프트맥스 회귀에서는 cost function으로 categorical cross entropy를 이용한다. Categorical cross entropy는 아래와 같은 식이며, pj는 예측값, qj는 실제값을 의미하며 j는 one hot vector의 인덱스 넘버이다.

이를 n개의 전체 데이터의 평균에 적용한다면 아래와 같다.

아래의 예시들을 통해 cost를 직접 계산해 보자.

위 식에 cost function을 적용하면 아래와 같다.
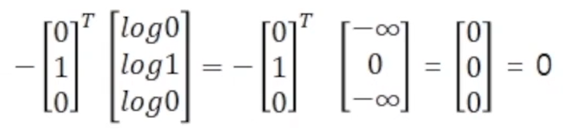
예시 1에서는 예측값이 실제값과 같아 cost가 0이 되는 것이다. 그렇다면 예측값과 실제값이 전혀 다른 경우엔 cost가 어떻게 변화하는지 살펴보자.

위와 같이 예측값과 실제값이 전혀 다른 경우 cost의 값이 무한대가 나왔다.
그렇다면 예측값과 실제값이 조금만 다른 경우는 cost가 어떻게 나올지 계산해보자.

위와 같은 cost가 나왔으며, 예측값이 결과값과 비슷할수록 cost의 값이 적어진다.
Cost의 값을 줄여 나가는 방향으로 최적화를 시키는데, 이 최적화 방법에는 경사하강법과 선택적 경사하강법, momentum등이 존재한다.
6. 종속변수 y의 개수가 2개일 때의 소프트맥스 회귀와 로지스틱 회귀

종속변수 y가 2개일 때 소프트맥스 회귀의 cost function과 로지스틱 회귀에서의 cost function은 같은 식이 된다. Y1을 y, y2를 1-y로 치환하고 p1을 p, p2를 1-p로 치환한 뒤 k의 값(클래스 개수)을 2로 두면 두 식은 결과적으로 같은 식이 나온다.
군집분석
1. 군집분석
: 비지도 학습의 한 종류로, 군집에 속한 데이터들의 유사성과 서로 다른 군집에 대한 데이터 간의 상이성을 규명하는 분석 방법이다. 군집 내 응집도가 최대화되며, 군집 내 분리가 최대화되어야 한다.
군집 분석의 목적은 관찰치들의 유사성을 측정한 후 가까운 순서대로 관찰치들을 군집화 한다. 관찰치의 유사성 측정 방법은 거리와 상관계수로 측정하는데, 두 개체 사이의 거리를 구하는 방법은 다음과 같다.
<두 개체 사이의 거리 구하는 공식 3가지>
1) 맨하튼 거리

2) 유클리디안 거리

주로 표준화된 자료에 이용한다.
3) 민코우스키 거리

거리 행렬로 군집 간의 유사성을 측정해 모든 데이터가 하나의 군집으로 병합될 때까지 반복해 군집화를 수행한다.

군집 분석은 한 군집이 다른 군집에 포함될 수 있느냐 없느냐, 즉 포함관계의 유무에 따라 계층적 군집과 비계층 군집으로 나뉜다.
1) 계층적 군집
: 한 군집이 다른 군집에 포함될 수 있는 군집.
계층적 군집의 군집화 방식엔 1) 최단 연결법, 2) 최장 연결법, 3) 평균 연결법, 4) ward 연결법 등이 존재한다. 우리는 최단 연결법을 살펴볼 것이다.
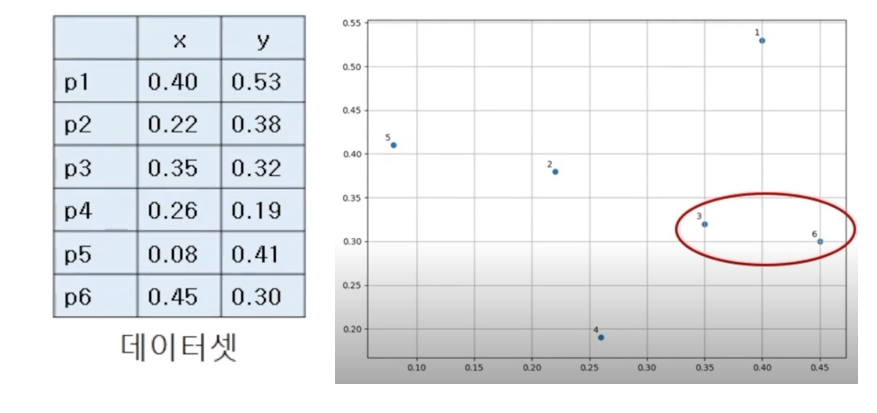
위와 같은 데이터 셋이 있고, 이를 그래프로 표현한 것이 우측 상단의 그래프이다.
데이터 샘플끼리의 거리는 유클리디안 거리법을 사용했으며, 그 예로 p1, p2의 거리를 계산하였는데 아래와 같이 약 0.24라는 값이 도출되었다.

위와 같은 방법으로 각 데이터 샘플끼리의 거리를 계산해보면 아래와 같은 거리 행렬이 나온다.
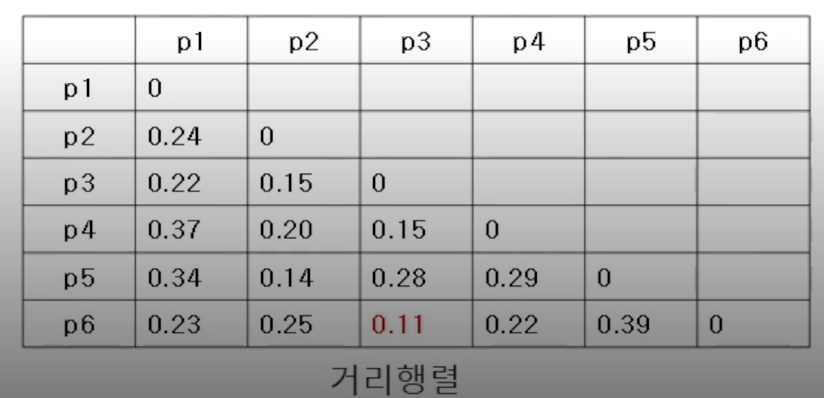
이 테이블에 있는 값 중 가장 작은 값을 선택하고, 이 작은 값에 해당하는 포인트가 군집이 된다. 현재 가장 작은 값은 0.11로, 이 0.11에 해당하는 p3와 p6가 하나의 군집으로 병합되었다.
병합된 군집 p3,p6는 하나로 취급한다. 따라서 새로 만든 거리 행렬은 아래와 같다.

포인트와 포인트의 거리를 비교하는 것은 유클리디안 식을 이용하면 되지만, 각 포인트들을 p3,p6로 묶인 군집과 거리를 비교할 때는 어떤 방법을 써야 할까?


위와 같이 포인트들을 군집 p3,p6와 비교해 더 작은 값이 나오는 포인트를 찾아내면 된다.
거리 행렬에서 가장 작은 값이 0.14로 두번째 군집은 p2와 p5가 병합된 군집이 되었다. 따라서 현재까지는 하단의 두 군집으로 데이터가 묶인 상태이다.

P2, p5의 군집과 p3,p6의 군집으로 된 다음 거리 행렬을 구하면

이러한 거리 행렬이 도출되고, 이 거리 행렬을 만드는 데 이용되는 군집과 군집 사이의 거리 식은 아래와 같다.

거리 행렬을 보면 가장 작은 값이 0.15인데, 0.15의 값이 2개가 존재한다. 이런 상황일 때는 어떠한 포인트를 골라 군집화해도 같은 결과가 나온다. 우리는 p2, p5, p3, p6가 병합된 군집을 만들기로 한다.

상단의 그래프와 같은 군집이 만들어지며, p2,p5,p3,p6의 군집으로 이루어진 거리 행렬을 만들어보자.

위 행렬에서 가장 최소값이 0.15이므로 이번엔 p2, p5, p3, p6와 p4를 병합한 군집이 새로 만들어진다.

이제 병합해야 할 남은 포인트는 p1하나가 존재한다.

위의 거리 행렬에서는 값이 하나 존재하기 때문에 이 0.15라는 포인트를 선택하고, 이제 p1,p2,p3,p4,p5,p6가 하나의 군집으로 병합된다.
dendrogram으로 이 계층적 군집화를 살펴보자.

제일 먼저 p3와 p6가 한 군집으로 묶이고, 그 뒤 p2, p5 -> p4,p2,p5,p3,p6 -> p1,p4,p2,p5,p3,p6의 순서대로 군집화해 하나의 군집으로 병합된 것이다.
2) K-means clustering(비지도 학습)
: 주어진 데이터를 소수의 그룹으로 나누는 방법이며, lable(y값)이 없어 입력 데이터인 x값이 lable역할을 한다. 기계학습에서 비지도 학습의 기법이며 군집 데이터들의 평균값으로 계산해서 중심을 찾는다. 사용자가 군집의 개수인 k를 직접 설정한다.
어떤 데이터 셋이 있고, k개의 클러스터로 분류하겠다고 가정하면, 그 데이터 셋에는 k개의 클러스터가 존재한다. 각 데이터들은 유클리디안 거리를 기반으로 가까운 중심에 할당되고, 같은 중심에 모인 데이터 그룹이 하나의 클러스터가 된다.
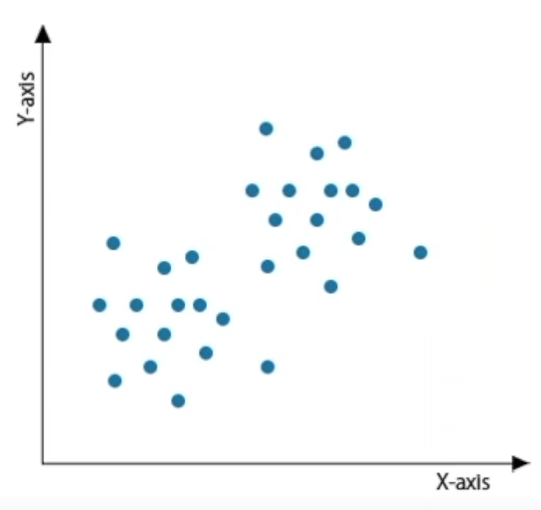
위와 같은 데이터들을 k-means clustering을 통해 k개의 군집으로 나눌 수 있다.
<k-means clustering의 알고리즘>
(1) 사용자가 데이터를 나눌 클러스터의 개수를 지정
(2) 사용자가 지정해준 군집의 개수 k개만큼 무작위로 중심점을 지정(가장 기본적인 알고리즘은 랜덤 초기화)
(3) 모든 데이터 셋과 각 중심과의 유클리디안 거리를 구해 데이터를 가장 가까운 중심에 할당한다. 이를 expectation단계라고 한다.
(4) k개로 나뉘어진 클러스터들에서 임의로 설정된 중심을 실제 클러스터의 중심이 되도록 다시 중심을 설정한다. 즉, 한 클러스터 내의 거리의 평균값을 다시 중심으로 설정하는 것이다.
(5) (3),(4)번을 반복한다. 새롭게 설정된 중심과 모든 데이터 셋까지의 유클리디안 거리를 구해 가장 가까운 중심에 데이터를 할당하고, 할당된 데이터로 이루어진 클러스터에서 평균 거리를 구해 새로운 중심을 찾는 것을 반복하면 된다.
이 과정을 하나의 예시를 통해 적용해보도록 하자.

(1) 그림1과 같이 주어진 데이터 셋이 있고, 분류할 클러스터의 개수 k를 3이라고 지정하면 그림2와 같이 3개의 점이 무작위로 중심점이 된다.
(2) 이 중심점과 random centroids(무작위 중심)간의 유클리디안 거리를 측정해 가장 가까운 중심에 데이터를 할당하면 그림3이 나온다.
(3) 그림 4에서 보듯이 이제 각 클러스터에 해당하는 데이터의 평균을 구해 그 평균이 새로운 중심점이 된다.
(4) 그림5처럼 새 중심점과 데이터 셋 간의 유클리디안 거리를 구한 뒤 가장 가까운 중심에 데이터를 할당한다. 이렇게 최종적으로 클러스터가 나뉘게 된다.