수학팀:김정민 박형준 최웅준 구예인 김경태
2020년 8월 20일 온라인 스터디

확률변수와 확률질량함수는 엄연히 다른것이다.
P(X=x)+P(Y=y)
x에 관한 함수
y에 관한 함수
x+y의 확률질량함수를 구하고 싶으면
x+y가 확률변수여야 합니다.
x+y에 관한 함수가 필요한 것 입니다.
'지도는 영토가 아니다'
확률변수는 집이다.
분포는 집의 설계도 입니다.
하나의 설계도를 가지고 여러개의 집을 만들 수 있습니다.
X ~bern
Y ~bern
아주 많은 다른 확률 변수들이 같은 분포를 가질 수 있습니다.
독립적일 수도 있고 독립적이 아닐 수도 있습니다.
포아송 분포
표기법
X~Pois(λ)
PMF

P(X=k)=e^-λ * λ^k / k!
k는 영이 아니다
λ는 비율 파라미터

포아송 분포의 기댓값
기댓값: 값과 확률의 곱의 합이다.

포아송 분포의 기댓값은 λ가 된다.
포아송 분포가 왜 중요할까요?
포아송분포는 실제 이산형 데이터의 모델로 가장 많고 널리 쓰이는 분포입니다.
수를 세는 응용에서 쓰입니다.
음수가 아닌 정수니까
어떤 숫자를 센다고 할 때 성공의 수를 세는 응용이라고 생각해봅시다.
이항분포처럼 성공과 실패는 일반화된 의미를 가집니다.
많은 시도를 하는데 각 결과는 성공 또는 실패입니다.
많은 시도와 아주 낮은 성공확률을 자긴 응용이어야 합니다.

한시간 안에 받은 이메일 갯수
이게 왜 포아송 분포일까
이메일을 보낼 수 있는 사람은 많다.
하지만 주기적으로 이메일을 보내는 사람이 아니면
각 사람이 당신에게 이메일을 보낼 확률은 매우 낮다.
초콜릿 칩 쿠키 안에 든 칩의 개수
쿠키 반죽으로 시작해서 칩을 몇개 만들고
모든 반죽이 초콜릿 칩인것은 아니다.
초콜릿 칩이 있을 있을 수 있는 조각은 많다.
Rain drop

Poisson Paradigm
실제로 포아송 분포를 쓰일 때는 상한이 있지만
이론에서는 무한대로 간다. k={0,1,2,3,4,5,6...}
하지만 대부분의 경우에는 추정하기 유용한 분포일것이다.
==>포아송 근사 혹은 pois Paradigm 이라고 부른다.
사건 A1,,,An
P(Aj)=pj
n은 큰수이고, pj는 작고,
각 사건들은 독립이거나 "약하게" 의존하는 경우
Aj의 발생 횟수가 포아송 분포에 근사한다고 주장할 수 있다.
여기서 람다(λ)가 포아송 분포의 기댓값이므로
Aj의 발생 횟수의 기댓값이 되는것이다.
사건이 의존적이여도 선형성에 의해 Aj의 발생횟수의 기댓값은 pj의 합과 같다.

이항분포의 포아송분포 수렴
지금까지는 각 사건이 독립적이고
각 사건의 발생 확률 p가 동일한 베르누이 분포기에
사건 발생 횟수가 p 확률의 이항분포였다.
이항분포(n,p)가 포아송 분포로 수렴한다는것을 증명해보자.
포아송 분포는 이항분포보다 훨씬 일반적이다.
즉, 이항분포를 만족하면 포아송 분포를 만족한다는것
(포아송 분포의 경우 p가 달라도 되고 조금의 의존성도 허용된다.)



n을 극한으로 보내면
n->∞
λ/n->0
k!는 상수
n(n-1)...(n-k+1)/n^k=e^-λ



이산확률변수 vs 연속확률변수


확률밀도함수(Probablity Density Function)[PDF]

연속확률변수에서 PMF(확률질량함수)를 사용하게 되면 모든값이 0일것이다.
그래서 확률밀도함수가 필요한데
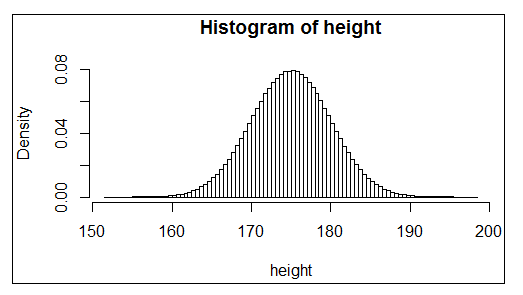
확률변수 X가 모든 a,b에 대하여
P(a<=X<=b)=integral a~b (f(x)) dx 를 만족시킬 때,
X는 확률밀도함수(PDF) f(x)를 갖는다.
a=b 인 경우, integral a~a (f(x)) dx = 0
조건
f(x)>=0, integral ∞~∞ f(x) dx = 1
이산확률변수에서는 확률을 질량이라고 생각했었죠.
조약돌로 비유해서 조약돌의 질량이 다 더해서 1이라고 했었는데
연속분포에선는 더이상 조약돌이라고 생각할 수 없습니다.
이제는 바닥에 문질러 있는 진흙입니다.
진흙의 총질량은 1입니다.
밀도라 하면 부피당 질량이 생각 나겠죠
f(x)를 적분하면 확률이 나옵니다.
a=b 인 경우, integral a~a (f(x)) dx = 0
이었으므로 특정값을 가질 확률은 0입니다.
확률밀도함수는 확률이 아니다.
1보다 큰 값을 가진 함수를 적분해서 1이 나올 수도 있기 때문입니다
확률을 구하고 싶다면 확률밀도함수를 특정 범위에서 적분하면 됩니다.
ε은 그냥 작은게 아닙니다 엄청나게 작은겁니다
그 작은 범위 안에서 f의 값은 크게 변하지 않는다는 것입니다
그 작은 범위 안에서 f가 상수함수가 되는 겁니다
'밀도'는 무엇인가?
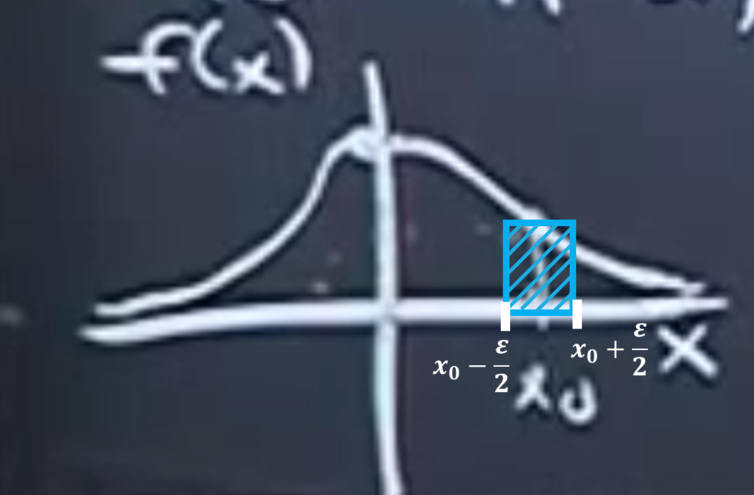


X가 PDF f를 가질 때

X가 CDF Fx(x)를 가질 때, PDF는 f(x)=F'x(x) 이다.
(연속적이지만 미분 가능하지 않은 함수가 존재합니다그러면 아주 복잡해지므로 연속확률변수라 함은 누적분포 함수가 미분 가능하다고 가정한다.)
<미적분학의 기본정리>

기댓값은 그냥 평균이죠
기댓값을 가지고는 분포의 폭이나 범위,분산에 대해서는 전혀 모릅니다.
그래서 분산이라는 개념이 필요한것이지요.
분산은 분포의 퍼짐의 정도를 알려줍니다.
분포들의 값이 그 분포의 평균으로부터 얼마나 떨어져 있는지를 알려줍니다.
기댓값에서 x를 빼는것부터 시작합시다.

절대값을 쓰면 되지만 V 모양이 나와서 미분할 수 없습니다.
절대값을 쓰는 대신 전체를 제곱할 수는 있죠.
제곱을 하면 미분이 가능하고
피타고라스 정리가 생각이납니다.
기하학이 존재하게 됩니다.
하지만 제곱을 하게 되면 단위가 바뀌죠
x의 단위가 마일이라면 마일의 제곱이 단위가 되겠죠
그래서 표준편차라는 개념이 생겼습니다.
루트를 씌워줌으로써 단위가 돌아오게 되죠
분산이 수학적으로 다루기 편하지만 '해석'을 위해서 표준편차를 사용하는것입니다.
균등분포(uniform distribution)
Unif(a,b) -> 모수
균등분포는 특정 범위가 뽑힐 확률이 그 범위의 크기에 비례하는 분포입니다.
크기가 같은 두 범위가 있을 때 각 범위가 뽑힐 확률이 같아야 합니다.
범위 안에서는 확률밀도가 같아야 합니다.
확률밀도가 다르다면 균등하지 않겠죠
PDF f(X)=c
c는 뭘까요?
확률밀도함수를 적분했을 때 1이 나와야 합니다.
a~b까지만 적분하면 되죠
이외의 부분은 0이니까
c=1/(b-a)가 됩니다.
1/범위의 크기이 되는것입니다.
CDF
확률밀도 함수를 -infinite~x까지 적분하면 되지만
아까와 같이 a~b까지 적분해도 값은 똑같습니다.
a와 b값에 따라서 CDF값은 달라집니다.
기댓값 또한 a에서 b까지 PDF값 * x 값을 곱한것을 적분해주면 됩니다.
결과적으로 그냥 중간값이 됩니다.
균등분포인데 당연한 결과입니다.
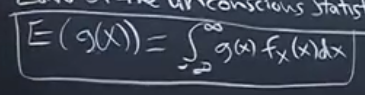
무의식의 통계학
제대로 생각 안 해보고
그냥 대충 X를 X^2으로만 바꾸고
이런 생각 없이 하게 되는 것들을 말합니다.
확률변수 X의 확률밀도 함수를 알고
X의 함수의 기댓값을 구하려 할 때 생기는 일입니다
정석대 하자면 이 함수의 분포를 찾아야하지만
게으른 방식으로는 원래 X의 확률 밀도 함수를 그대로 쓰는것 입니다.

g(X)의 확률밀도함수를 구할 필요가 없습니다.
균등분포의 분산

E(u²)을 구하려면 무의식적인 통계학자의 법칙에 의해
u²의 확률밀도함수를 구할 필요는 없습니다
바로 u의 확률밀도함수를 써서 이 적분을 하면 됩니다


균등분포의 일반성(universality of the uniform distribution)
Unif(0,1) 를 통하여 어떠한 확률분포를 만들어낼 수 있다.
어떠한 분포든지 균등분포에서 그 분포로 전환할 수 있습니다.
대부분의 상황에서는 확률변수가 주어지고 누적분포함수를 구하지만
이번에는 특정 누적분포함수를 가진 분포를 만들어 보자.
F:누적분포함수
U∼Unif(0,1), CDF F를 가질 때 (F는 연속인 증가함수이다==>역함수 F^-1이 존재한다.)
정리) X = F^{-1}(U) 일 때, X∼F ===>역함수에 u를 넣은걸 X라고 했을 때 X가 F 분포를 따른다. X의 누적분포함수가 F가 되는것이다.
원하는 누적분포함수의 역함수를 구하고 확률변수를 넣으면 원하는 분포가 나오는것이다.
양쪽에 F를 취하게 되면 증명할 수 있다.
증명) P(X <= x) = P(F^{-1}(U)<= x) = P(U<=F(x))

문제풀이
https://projects.iq.harvard.edu/stat110/strategic-practice-problems
Strategic Practice and Homework Problems
Actively solving practice problems is essential for learning probability. Strategic practice problems are organized by concept, to test and reinforce understanding of that concept. Homework problems usually do not say which concepts are involved, and oft
projects.iq.harvard.edu
chapter5 poisson problem









'4기(20200711) > 수학 스터디' 카테고리의 다른 글
| 무의식적인 통계학자의 법칙(LOTUS) (0) | 2020.09.05 |
|---|---|
| 정규분포 (Normal Distribution) (0) | 2020.08.28 |
| 수학스터디[확률통계] [기대값][기하분포][음이항분포] (0) | 2020.08.14 |
| 수학스터디[확률통계] [확률변수] (0) | 2020.08.07 |
| 수학스터디[확률통계] [독립][조건부확률][전확률][몬티홀][심슨의 역설] (0) | 2020.07.31 |