*강화학습팀 / 발표자 조민성
- Polynomial Regression
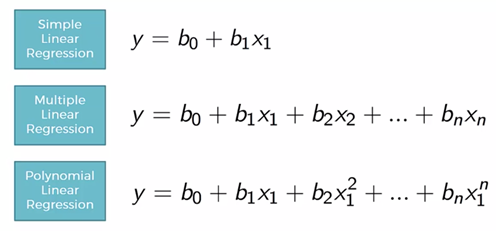
-Polynomial Neural Network(PNN)
:ANN은 Y = X^2 의 함수, 혹은 Y = X^X 의 함수를 근사할 수 있는가?
:평범한 ANN은 값을 근사하지만, 함수를 근사하지는 못한다! (Overfiting)
-GMDH란?
: Group method of data handling
: Polynomial 방식을 사용하여 함수를 근사시키는 휴리스틱
->GMDH를 ANN에 적용시키는 경우 PNN 구현 가능(상세는 PPT 참고)
->그렇다면 별도의 ANN Architecture의 변형없이 Polynomial의 구현이 가능한가?
1) X와 X*X를 인풋으로 함께 준다
: Y = 2*X*X + 1일 때, 뉴럴 네트워크가 인풋의 편향치를 조절
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.seq = nn.Sequential(
nn.Linear(2,524),
nn.ReLU(),
nn.Linear(524,1024),
nn.ReLU(),
nn.Linear(1024,1)
)
def forward(self, X):
return self.seq(X)
def train(model, train_set, label_set, optimizer, criterion):
total_cost = 0
x_pow = torch.stack([train_set, train_set*train_set]).transpose(1,0).reshape(-1,2)
optimizer.zero_grad()
output = model(x_pow)
loss = criterion(output, label_set)
total_cost += loss
loss.backward()
optimizer.step()
print(total_cost/64)
newmodel = Net()
optimizer = optim.Adam(newmodel.parameters(), lr = 0.0005)
criterion = nn.MSELoss()
for epoch in range(1000):
X = torch.randn(64,1)*10
Y = 2*X*X+1
train(newmodel, X, Y ,optimizer, criterion)
|
cs |
-> 실제로 Weight들이 X*X쪽으로 편향되었다.
-분석 : 문제는 제한적으로 유효하다. 즉 X*X가 최고차항인 경우에만 유효하다.
만일 최고차항의 지수가 5라면, 네트워크에 인풋으로 넣어야 하는 데이터 수가 5배로 늘어난다.
즉 비효율적
2)데이터는 그대로, 조절은 Activation function에서 한다.
: 위와 같이 Y = 2*X*X + 1일 때, 데이터는 그대로 주면서, 네트워크 내에서 값을 조절한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class newNet(nn.Module):
def __init__(self):
super(newNet, self).__init__()
self.linear1 = nn.Linear(1,524)
self.linear2 = nn.Linear(524,1024)
self.linear3 = nn.Linear(1024,1)
def forward(self, X):
output = self.linear1(X)
output = output*output
output = self.linear2(output)
output = F.relu(output)
return self.linear3(output)
def train(model, train_set, label_set, optimizer, criterion):
total_cost = 0
optimizer.zero_grad()
output = model(train_set)
loss = criterion(output, label_set)
total_cost += loss
loss.backward()
optimizer.step()
print('avg cost: ',total_cost/64,'\n')
newmodel = newNet()
optimizer = optim.Adam(newmodel.parameters(), lr = 0.001)
criterion = nn.MSELoss()
for epoch in range(1000):
X = torch.randn(64,1)*10
Y = 2*X*X+1
train(newmodel, X, Y ,optimizer, criterion)
|
cs |
->굉장히 깔끔하게 학습된다.
-분석 : 역시나 제한적으로 유효하다. 최고차항의 지수가 커지면 이 역시 사용하지 못한다.
흥미로운 사실은 ReLU와 output*output의 위치를 바꿔도 상관이 없으나,
둘 다 output*output으로 바꾸면 학습이 되지 않는다.
이유는 값의 증폭이 너무 커서 근사시키지 못하는 것으로 보인다.
'Monthly Seminar' 카테고리의 다른 글
| AI겨울과 미래 (0) | 2020.04.27 |
|---|---|
| Stereo R-CNN based 3D Object Detection for Autonomous Driving 논문 리뷰 (0) | 2020.04.18 |
| 얼굴 인식에 대해서 (0) | 2020.03.13 |
| 20.02.29 Monthly Seminar 자율주행자동차 (1) | 2020.03.02 |
| 웹크롤링 & 3.5기 프로젝트 시작 전 회의 (0) | 2020.02.29 |