발표자: 남서아
논문 원문 제목: On Empricial comparisions of optimizers for deep learning


이 논문에서는 첫 번째로 , Optimizer 간의 inclusive relationship( 포함관계)가 실제 practice 에서 영향을 준다는 것을 보입니다 . 그리고 하이퍼 파라미터 튜닝 프로토콜에 대한 옵티마이저 비교 민감도를 증명합니다 . 이전의 실험결과와 비교하는 것을 통해 , 주어진 워크로드 ( 모델과 데이터 set 쌍 ) 으로 optimizer 랭크를 바꾸기 쉽다는 것 또한 증명합니다 .

이 연구가 실행된 배경은 윌슨 앳 알 이라는 2017년 논문과, 슈네이드 엣 알이라는 2019년의 논문에서 허점을 발견한 것으로부터 시작됩니다. 그들은 ADAM, 즉 adaptive gradient methods 를 사용해여 간단한 분류 문제를 구성했는데, 여기에서 그들은 learning rate와 learning rate decay 등 하이퍼 파라미터의 subset만 변경시키고,등 다른 하이퍼 파라미터들은 바꾸지 않고 모두 고정된 기본값으로만 설정했습니다. 이것 외의 여러 학술자료들과 비교해본 결과, 하이퍼 파라미터 튜닝을 통해 더 좋은 결과를 얻어낼 수 있을 것으로 생각하고 이 연구를 진행하게 되었습니다.

먼저 옵티마이저가 무엇인지를 알아야합니다. 물론 다 아시겠지만, 옵티마이저는 local minimum 또는 global minimum을 찾는 것을 목표로 합니다. 여기에서 나온 편미분함수 그래디언트 엘 세타는 뉴럴네트워크에 의해 계산된 손실함수로 봅니다. 이때 세타는 rd 공간 속 모델 파라미터의 벡터입니다. Optimizer들 사이의 차이점은 업데이트 룰 M과 하이퍼파라미터에 의해 결정되고, 튜닝할 하이퍼 파라미터의 선택은 효과가 나타나는 family를 결정합니다.

이제 optimize의 과정을 살펴보겠습니다. 보시는 슬라이드에 나온 것처럼 optimize의 1차 재귀 메소드는 이런 식을 진행됩니다. 그리고 옆을 보시면, 그것과 비교하여, SDN, 즉 stochastic gradient descent 알고리즘은 조금 다른 방식으로 진행되는 것을 확인할 수 있습니다. 확률적 경사하강법은 loss function을 계산할 때, 전체 데이터 대신 일부데이터의 모음인 mini-batch를 이용하여 계산하기 때문에 속도가 매우 빠르고 local minimum에 빠질 확률도 낮은 방법입니다. 모멘텀 파라미터와 learning rate를 하이퍼 파라미터로 갖습니다.

다음 그림은 각각 update rule(업데이트 규칙)을 통해 어떻게 1차적으로 재귀를 진행하는 지, Optimizer 종류 별로 수식을 보여준 그림입니다.

Optimizer에 대해 간략한 소개를 끝냈으니 이제 본론을 들어가도록 하겠습니다. 이 문서의 3.1 절에서는 The taxonomy of first-ordered methods를 설명합니다. 직역하자면, 1차 방식의 분류라는 뜻입니다. 여기에서 우선 알아둬야 할 점은, 어떤 optimizer들은 서로를 유사하게 근사할 수 있다는 점입니다. 예를 들자면 optimizer A는 optimizer B의 하이퍼 파라미터 설정 등의 것들을 유사하게 따라할 수도 있습니다. 이 개념을 설명하기 위해 여기에서는 Optimizer의 포함관계를 먼저 설명합니다. 슬라이드의 식을 한번 살펴볼수 있겠습니다. 1차 최적화 방식을 위한 업데이트 룰 M,N이 있다고 가정할 때, 저런 결과를 가정할 수 있습니다. 또, 아래의 조건식을 통해 optimizer간의 포함관계가 성립할 수 있음을 알 수 있습니다. 그동안의 학술연구 결과를 종합하면 이 3번째 사진과 같은 Optimizer간의 포함관계 식을 볼 수 있습니다.
이러한 포함관계는 하이퍼 파라미터의 조정을 유연하게 만들고, 많은 Optimizer 간 비교문제를 해결할 것으로 보입니다. 그러나 딥러닝 시행자에게 포함계층이 의미있는지는 보장해주지 않습니다. 예를 들어, ADAM을 MOMENTUM과 매치되거나 혹은 성능을 능가하게끔하는 하이퍼 파라미터가 있다고 하면, 그건 접근조차 쉽지 않습니다. 아주 큰 값으로 존재한다는 한계가 있기 떄문에, 아주 큰 연산량을 시행하는 사람이 아니면 찾기가 힘듭니다.

그럼, 다음으로 이어지는 실험 파트에서 포함관계가 실제로 어떻게 의미있는지를 알아볼 수 있겠습니다. 하이퍼 파라미터 탐색공간(search space)를 각각의 optimizer 공간에 선정하는 것은 optimizer들을 실증적으로 비교하는 데 핵심적인 선택입니다. 선행된 연구들은 각각의 optimizer들을 모두 같은 탐색공간을 사용하게 하여 옵티마이저들을 고르게 처리하려고 했습니다. 그러나 그건 비슷한 이름을 가진 하이퍼파라미터가 옵티마이저 간에 비슷한 값을 가져가야만 한다는 추정을 내포한 것이기 때문에, 맞지 않았습니다.
그래서 이 실험에서는 각각의 옵티마이저에 상대적으로 큰 탐색공간을 선정하였습니다. 그리고 log 규모로 하이퍼 파라미터를 바꿔가며 값을 탐색했습니다. 그 결과 이러한 탐색 공간은 하이퍼파라미터의 탐색을 더 효율적으로 하게 해준다는 결론을 도출할 수 있었습니다

자 그럼 또 다음의 4.1절, 워크로드에 대한 오버뷰와 실험의 세부사항을 살펴봅니다. 이 연구는 언어의 모델링과 이미지 분류에서 옵티마이저들의 상대적인 성능을 조사하였습니다.

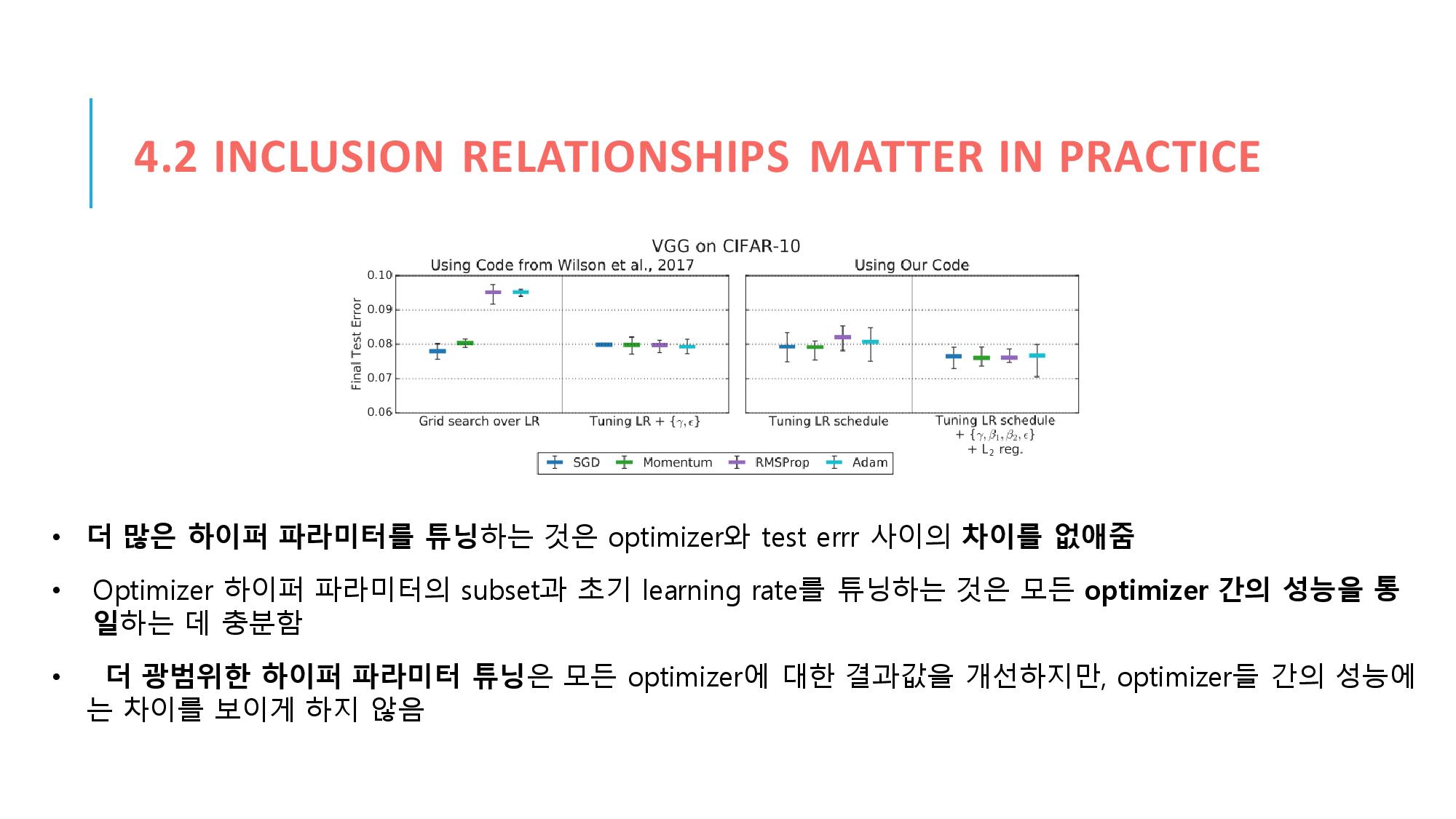


4.3 절에서는 이 연구가 이전의 윌슨이나 슈네이더 등의 연구들과 하이퍼파라미터 튜닝 프로토콜이 다른 결과를 보인다를 증명하려고 합니다. 여기서는 그들의 연구에 쓰인 대표적인 subset들의 결과를 실패시키거나 역으로 뒤짚어서 새로운 대표적 subset을 만들어 냈습니다. 그리고 그건 하이퍼 파라미터 탐색 공간을 확장시키는 것만으로 옵티마이저 랭킹을 만들어서 가능해졌습니다. 그리고 이걸 통해 ADAM이 하이퍼 파라미터만 모두 조율시키면 MOMENTUM보다 더 성능이 좋아질 수 있음을 보았습니다. 이전의 연구보다 더 충분한 하이퍼 파라미터를 튜닝시킴으로서 ADAM의 결과를 좀더 즉각적으로 명확하게 만들 수 있었습니다
마지막으로 추가 자료화면을 설명하겠습니다.
도표 1에서는 이 연구에 사용된 옵티마이저들의 업데이트 규칙과 포함관계를 옵티마이저 별로 서술합니다.



B로 넘어가면, 모델과 데이터 셋, 즉 워크로드를 어떻게 구성했는지 정보들을 소개하고 있습니다.

C에서는 bootstrap 기법을 이용해서 trial outcome을 추정했음을 설명합니다. 참고로 부트스트랩은 샘플링 분포를 추정하기 위한 샘플링 기법입니다. 랜덤 샘플링을 통해 training data를 늘리는 방법입니다.데이터 셋(training set) 내의 데이터 분포가 고르지 않은 경우에 사용되기도 합니다.
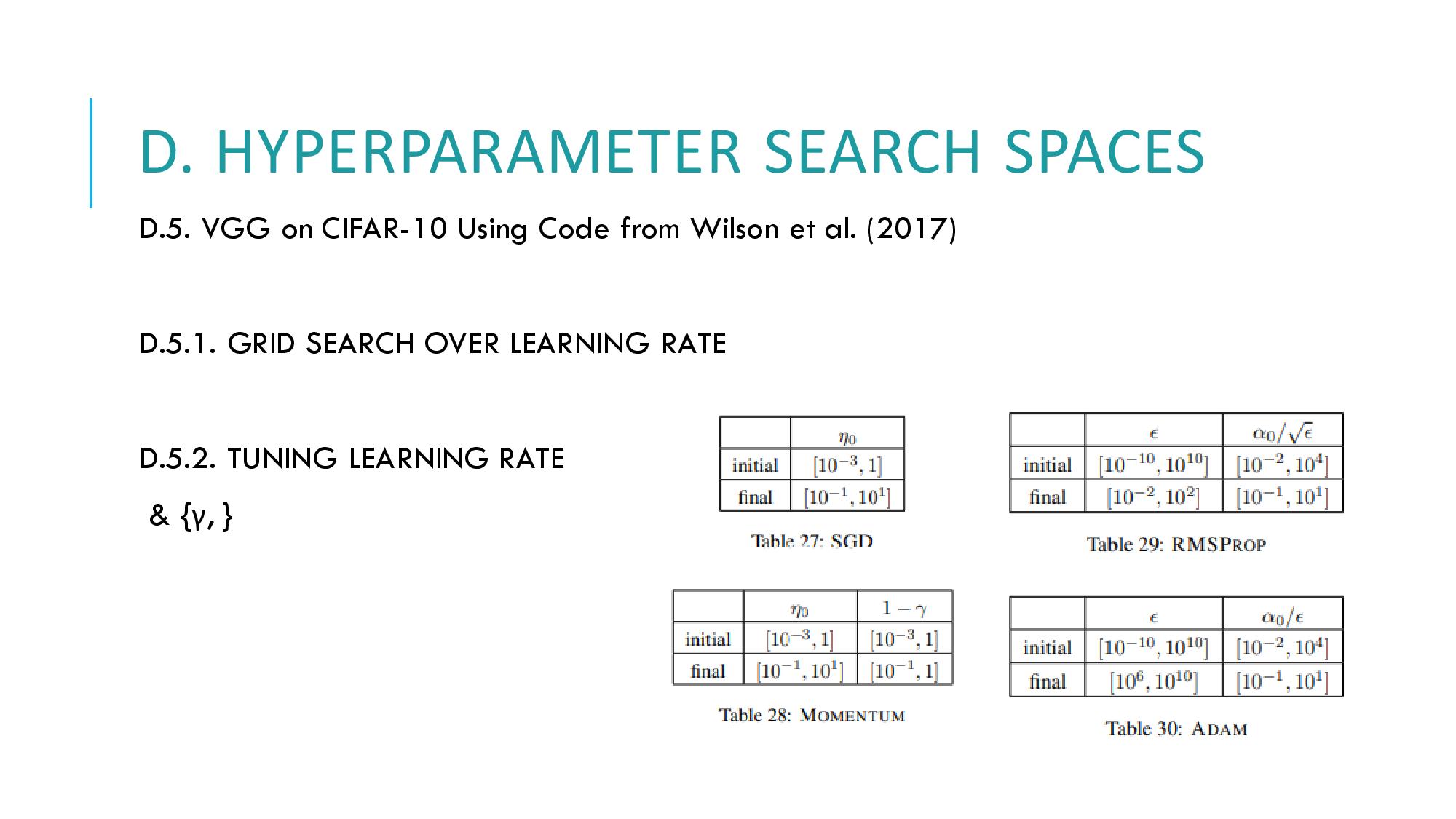
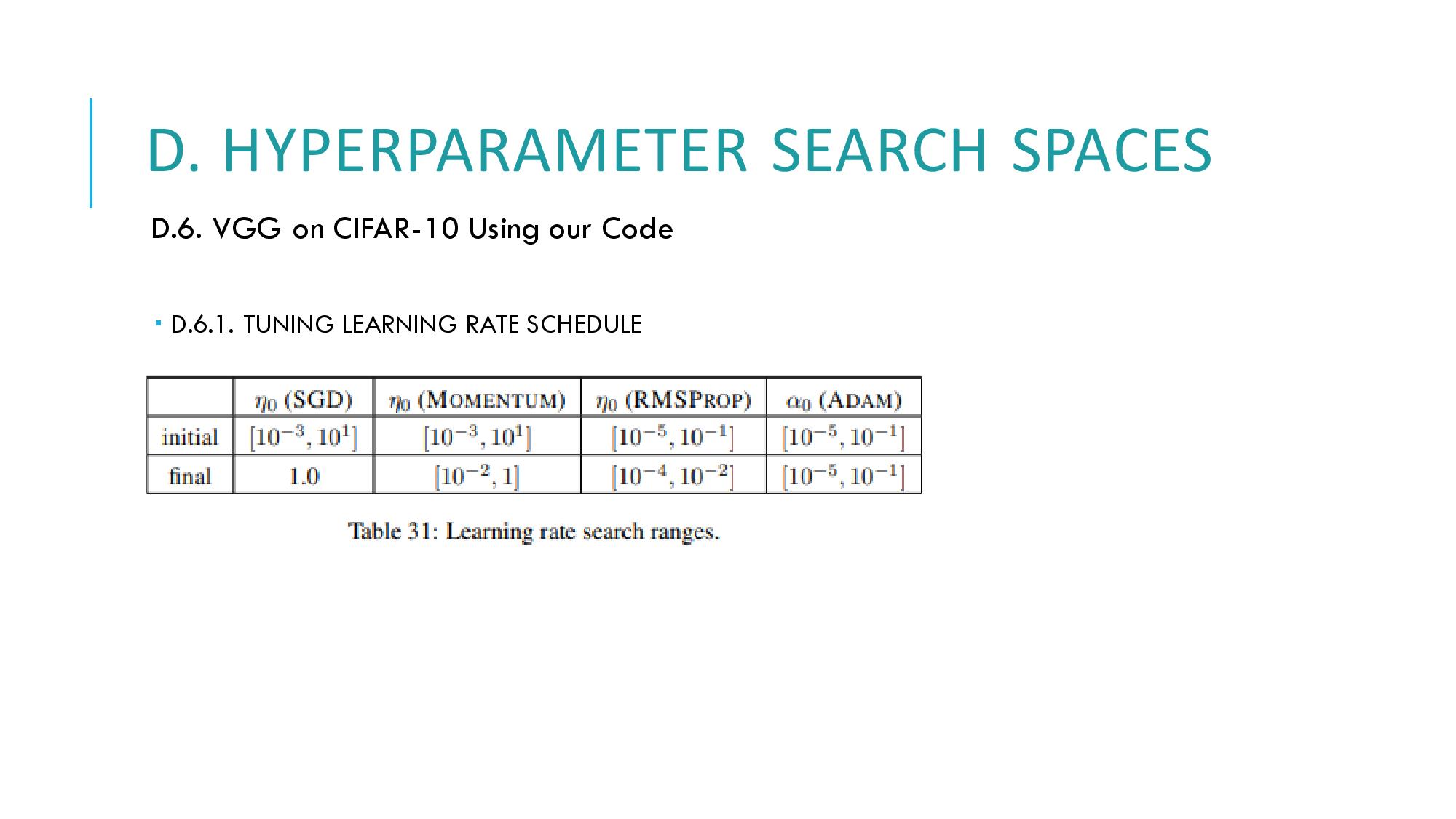
D에서는 decay step, learning rate decay 등의 튜닝에 따라 하이퍼 파라미터 탐색 공간이 어떻게 튜닝되었는지 결과값을 보여줍니다.








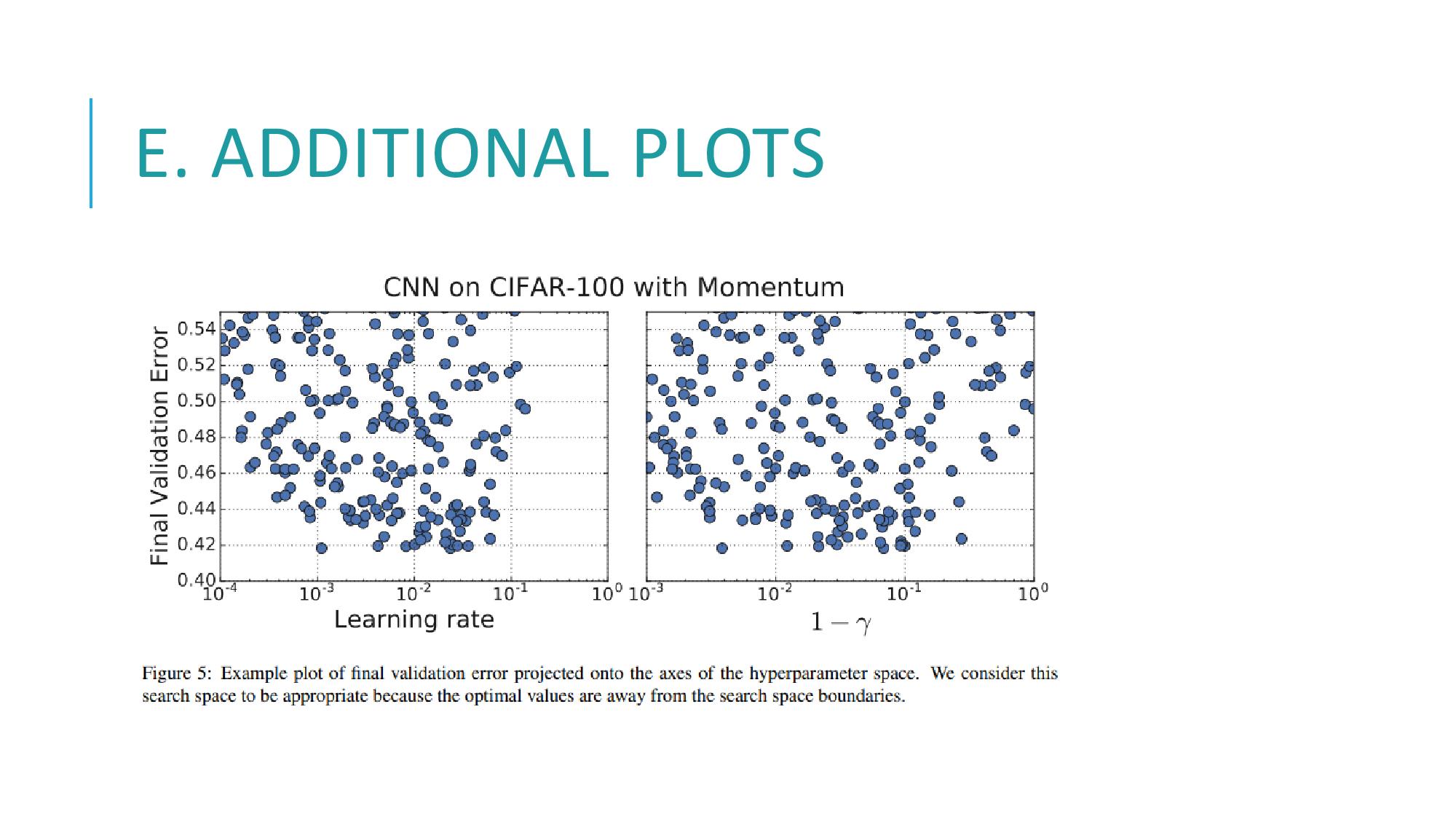
E에서는 하이퍼파라미터 공간에 투영된 final validation error의 example plot을 보여줍니다 이 탐색공간은 적절하다고 볼 수 있는데, 그 근거는 최적값들이 seraching space(탐색공간)의 경계에서 떨어져 있기 때문입니다.

figure 6에서는 best trial에서의 validiation 성능이 2의 4승 하이퍼파라미터 튜닝 trial에서 수렴한다는 것을 보여줍니다. figure 7에서는 CNN과 ResNet-50에서도 best trial의 validiation 성능이 2의 4승에서 수렴함을 보여줍니다.

Figure8에서는, war and peace의 2-레이어 LSTM에서도 best trial의 validation 성능이 2의 3승에서 수렴함을 보여줍니다. 여기에서, figure 6에서 8까지의 그래프는 모두 bootstrap으로 샘플링했습니다

Figure 9에서는 옵티마이저간의 상대적인 성능이 우리가 가장 낮은 training loss를 선택할 경우, 포함관계에서 일정하게 나타남을 보여줍니다. 그 이유는 그들의 final 탐색공간이 validation error를 최소화하기위해 optimized 된 것이기 때문입니다.
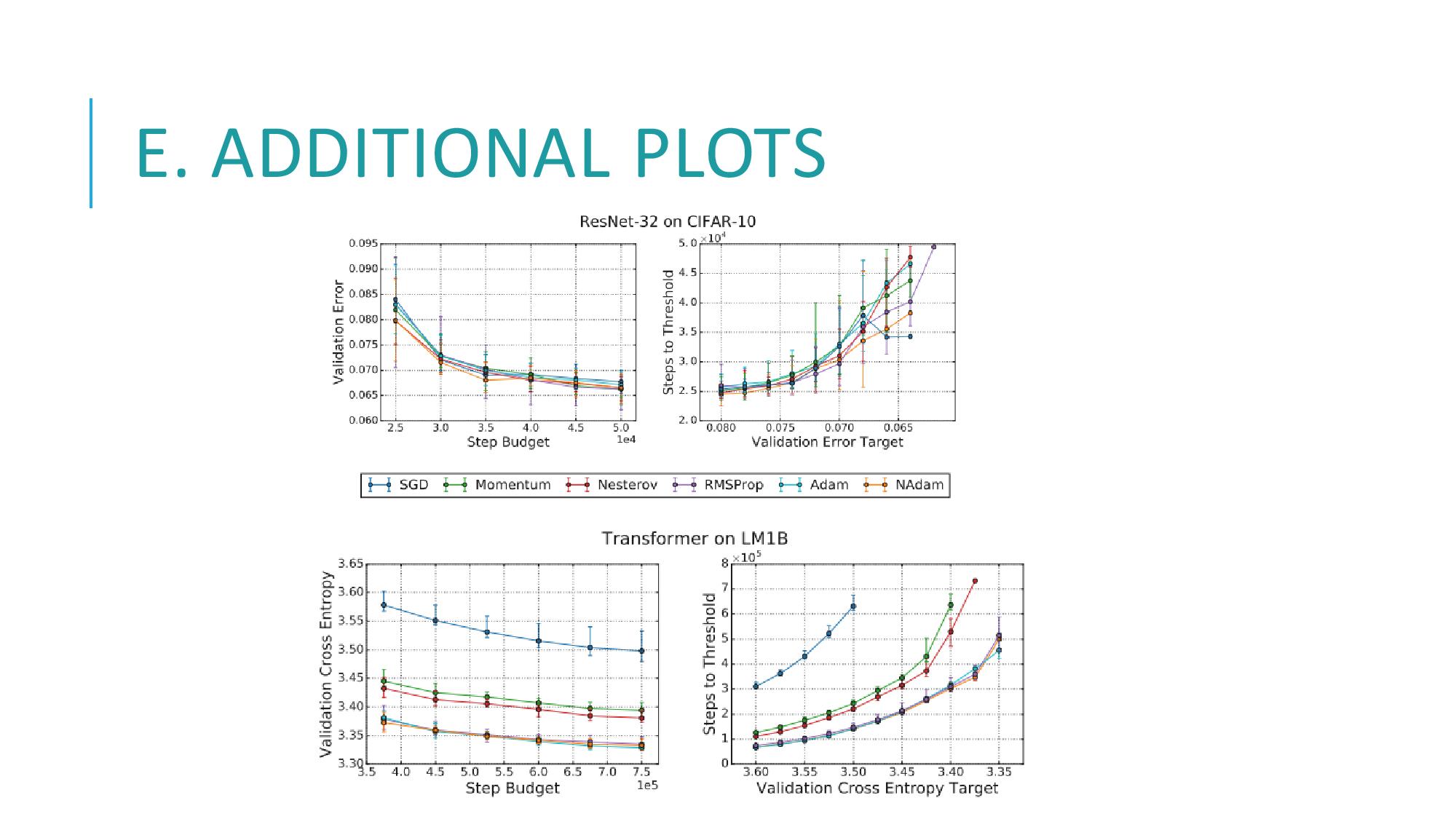
마지막으로 figure 10은 옵티마이저 포함관계 간의 연관성이, 우리가 선택한 정확한 step 단위나 error 타겟에 의존하지 않음을 보여줍니다.
이상으로 발표를 마칩니다 감사합니다.
'4기(20200711)' 카테고리의 다른 글
| YOLO, YOLOv3 논문 리뷰 (0) | 2020.12.05 |
|---|---|
| SqueezeNet [모델 압축] 논문 리뷰&구현 [Matlab] (0) | 2020.11.18 |
| 11/07 세미나 [Decoupled Neural Interfaces using Synthetic Gradients] & [Layer Nomalization] (0) | 2020.11.07 |
| 10/24 졸업생 발표 세미나 (0) | 2020.10.31 |
| 10/10 신촌 오프라인 세미나 [ALEXNET,RESNET] (0) | 2020.10.31 |